
【题目】如图,![]() 是
是![]() 的弦,
的弦,![]() 经过圆心
经过圆心![]() ,交
,交![]() 于点
于点![]() ,
,![]() .
.
(1)直线![]() 是否与
是否与![]() 相切?为什么?
相切?为什么?
(2)连接![]() ,若
,若![]() ,求
,求![]() 的长.
的长.
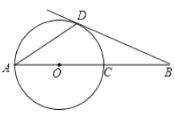
【答案】(1)相切,证明详见解析;(2)15
【解析】
(1)连接OD,根据三角形的内角和求出∠ADB,再根据半径相等得出∠A=∠ADO=30°,即可得出答案;
(2)连接CD,求证△ODC是等边三角形,再证CD=CB,即可得出答案.
(1)证明:连接OD
∵![]()
∴∠ADB=180°-∠DAB-∠B=120°
又OA=OD
∴∠A=∠ADO=30°
∴∠ODB=∠ADB-∠ADO=90°
∴直线![]() 与
与![]() 相切
相切
(2)连接CD
∵∠A=30°
∴∠DOC=60°
又OD=OC
∴△DOC是等边三角形
∴OD=OC=CD=5,∠ODC=60°
∴∠CDB=∠ODB-∠ODC=30°
又∠B=30°
∴∠B=∠CDB
∴CB=CD=5
∴AB=AC+CB=2OC+CB=10+5=15


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=-x2+bx+c与直线AB交于A(-4,-4),B(0,4)两点,直线AC:y=-![]() x-6交y轴与点C.点E是直线AB上的动点,过点E作EF⊥x轴交AC于点F,交抛物线于点G.
x-6交y轴与点C.点E是直线AB上的动点,过点E作EF⊥x轴交AC于点F,交抛物线于点G.
(1)求抛物线y=-x2+bx+c的表达式;
(2)连接GB、EO,当四边形GEOB是平行四边形时,求点G的坐标;
(3)①在y轴上存在一点H,连接EH、HF,当点E运动到什么位置时,以A、E、F、H为顶点的四边形是矩形?求出此时点E、H的坐标;
②在①的前提下,以点E为圆心,EH长为半径作圆,点M为⊙E上一动点,求![]() AM+CM的最小值.
AM+CM的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() (
(![]() )的图象与x轴交于点A(﹣1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(包括这两点),下列结论:
)的图象与x轴交于点A(﹣1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(包括这两点),下列结论:
①当x>3时,y<0;
②3a+b<0;
③![]() ;
;
④![]() ;
;
其中正确的结论是( )
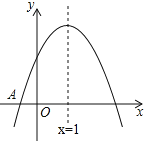
A.①③④B.①②③C.①②④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
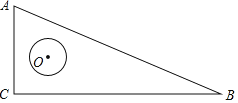
【题目】如图,在△ABC中,AC:BC:AB=5:12:13,⊙O在△ABC内自由移动,若⊙O的半径为1,且圆心O在△ABC内所能到达的区域的面积为![]() ,则△ABC的周长为_____.
,则△ABC的周长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在△ABC中,如果正方形PQMN的边QM在BC上,顶点P,N分别在AB,AC上,那么我们称这样的正方形为“三角形内接正方形”小波同学按数学家波利亚在《怎样解题》中的方法进行操作:如图(2),任意画△ABC,在AB上任取一点P′,画正方形P′Q′M′N′,使Q′,M′在BC边上,N′在△ABC内,连结BN′并延长交AC于点N,画NM⊥BC于点M,NP⊥NM交AB于点P,PQ⊥BC于点Q,得到四边形PQMN,小波把线段BN称为“波利亚线”,请帮助小波解决下列问题:
(1)四边形PQMN是否是△ABC的内接正方形,请证明你的结论;
(2)若△ABC为等边三角形,边长BC=6,求△ABC内接正方形的边长;
(3)如图(3),若在“波利亚线”BN上截取NE=NM,连结EQ,EM.当![]() 时,猜想∠QEM的度数,并说明你的理由.
时,猜想∠QEM的度数,并说明你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,t的值为
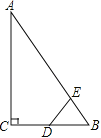
A、2 B、2.5或3.5 C、3.5或4.5 D、2或3.5或4.5
查看答案和解析>>
科目:初中数学 来源: 题型:
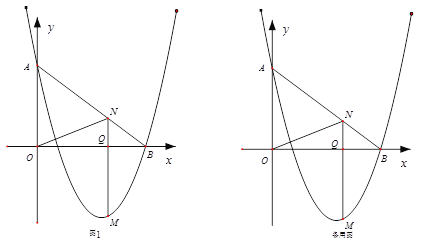
【题目】如图1,在平面直角坐标系中,![]() 为坐标原点.直线
为坐标原点.直线![]() 与抛物线
与抛物线![]() 同时经过
同时经过![]() .
.
(1)求![]() 的值.
的值.
(2)点![]() 是二次函数图象上一点,(点
是二次函数图象上一点,(点![]() 在
在![]() 下方),过
下方),过![]() 作
作![]()
![]() 轴,与
轴,与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .求
.求![]() 的最大值.
的最大值.
(3)在(2)的条件下,是否存在点![]() ,使
,使![]() 和
和![]() 相似?若存在,求出
相似?若存在,求出![]() 点坐标,不存在,说明理由.
点坐标,不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下表:
x | 0 | 1 | 2 |
ax2 |
| 1 |
|
ax2+bx+c | ﹣3 |
| ﹣3 |
(1)求a、b、c的值,并在表内空格处填入正确的数;
(2)根据上面的结果解答问题:
①在方格纸中画出函数y=ax2+bx+c的图象;
②根据图象回答:当x的取值范围是 时,y≤0?

查看答案和解析>>
科目:初中数学 来源: 题型:
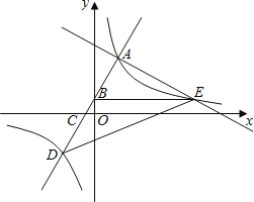
【题目】如图,直线y=2x+b与双曲线y=![]() (k>0)交于点A、D,直线AD交y轴、x轴于点B、C,直线y=-
(k>0)交于点A、D,直线AD交y轴、x轴于点B、C,直线y=-![]() +n过点A,与双曲线y=
+n过点A,与双曲线y=![]() (k>0)的另一个交点为点E,连接BE、DE,若S△ABE=4,且S△ABE:S△DBE=3:4,则k的值为___.
(k>0)的另一个交点为点E,连接BE、DE,若S△ABE=4,且S△ABE:S△DBE=3:4,则k的值为___.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com