
若单项式 与
与 的和仍为单项式,则这两个单项式的和为__________.
的和仍为单项式,则这两个单项式的和为__________.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:云南省双柏县2017-2018学年八年级上期期末数学试卷 题型:单选题
下列说法正确的是( )
A. 要了解某公司生产的100万只灯泡的使用寿命,可以采用抽样调查的方法
B. 4位同学的数学期末成绩分别为100、95、105、110,则这四位同学数学期末成绩的中位数为100
C. 甲乙两人各自跳远10次,若他们跳远成绩的平均数相同,甲乙跳远成绩的方差分别为0.51和0.62,则乙的表现较甲更稳定
D. 某次抽奖活动中,中奖的概率为 表示每抽奖50次就有一次中奖
表示每抽奖50次就有一次中奖
查看答案和解析>>
科目:初中数学 来源:山东省东营市河口区2017-2018学年度第一学期期末考试九年级数学试卷 题型:解答题
(1)计算: 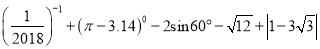 ;
;
(2)先化简,再求值:  ,其中x=4﹣tan45°.
,其中x=4﹣tan45°.
查看答案和解析>>
科目:初中数学 来源:山东省东营市河口区2017-2018学年度第一学期期末考试九年级数学试卷 题型:单选题
已知关于x的方程x2+3x+a=0有一个根为﹣2,则另一个根为( )
A. 5 B. ﹣1 C. 2 D. ﹣5
B 【解析】根据一元二次方程根与系数的关系,利用两根和,两根积,即可求出a的值和另一根. 【解析】 设一元二次方程的另一根为x1, 则根据一元二次方程根与系数的关系, 得﹣2+x1=﹣3, 解得:x1=﹣1. 故选B.查看答案和解析>>
科目:初中数学 来源:北京大学附属中学2017-2018学年七年级上学期期中考试数学试卷 题型:解答题
解方程:
(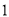 )
) .
.
( )
) .
.
查看答案和解析>>
科目:初中数学 来源:北京大学附属中学2017-2018学年七年级上学期期中考试数学试卷 题型:单选题
在密码学中,直接可以看到内容为明码,对明码进行某种处理后得到的内容为密码.有一种密码,将英文 个字母
个字母 ,
,  ,
,  ,
,  ,
,  (不论大小写)依次对应
(不论大小写)依次对应 ,
,  ,
,  ,
,  ,
, 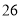 这
这 个自然数(见表格),当明码对应的序号
个自然数(见表格),当明码对应的序号 为奇数时,密码对应的序号
为奇数时,密码对应的序号 ,当明码对应的序号
,当明码对应的序号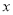 为偶数时,密码对应的序号
为偶数时,密码对应的序号 ,按下述规定,将明码“
,按下述规定,将明码“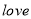 ”译成密码是:
”译成密码是:
字母 |
|
|
|
|
|
|
|
|
|
|
|
|
|
序号 |
|
|
|
|
|
|
|
|
|
|
|
|
|
字母 |
|
|
|
|
|
|
|
|
|
|
|
|
|
序号 |
|
|
|
|
|
|
|
|
|
|
|
|
|
A.  B.
B. 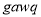 C.
C. 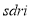 D.
D. 
查看答案和解析>>
科目:初中数学 来源:北京大学附属中学2017-2018学年七年级上学期期中考试数学试卷 题型:单选题
下列各式中,去括号正确的是( ).
A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:广东省广州市天河区2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
一般情况下,一个分式通过适当的变形,可以化为整式与分式的和的形式,例如:
① ;
;
②
(1)试将分式 化为一个整式与一个分式的和的形式;
化为一个整式与一个分式的和的形式;
(2)如果分式 的值为整数,求x的整数值.
的值为整数,求x的整数值.
查看答案和解析>>
科目:初中数学 来源:江苏省东部分校2017-2018学年八年级上学期期末考试数学试卷 题型:填空题
一次函数的图象经过点(-1,0),且函数值随自变量的增大而减小,符合要求的函数的解析式可以是:(写出一个即可)___________ .
y=-x-1(答案不唯一) 【解析】试题解析:设一次函数的解析式为y=kx+b(k≠0). ∵函数值随着自变量的增大而减小, ∴x的系数k<0,可定为-1, ∴函数解析式可表示为:y=-x+b,把(-1,0)代入得,b=-1, ∴要求的函数解析式为:y=-x-1.(答案不唯一). 故答案是:y=-x-1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com