
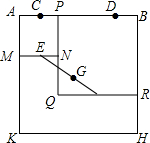
 如图,四边形ABHK是边长为6的正方形,点C、D在边AB上,且AC=DB=1,点P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作正方形AMNP和正方形BRQP,
如图,四边形ABHK是边长为6的正方形,点C、D在边AB上,且AC=DB=1,点P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作正方形AMNP和正方形BRQP,分析 设KH的中点为S,连接PE,PF,SE,SF,PS,由三角形相似结合E为MN的中点,S为KH的中点可得A,E,S共线,F为QR的中点,S为KH的中点得B,F,S共线,再由三角形相似得到ES∥PF,PE∥FS,结合G为EF的中点可得G为PS的中点,即G的轨迹为△CSD的中位线,由三角形的中位线长是底边的一半得答案.
解答 解:如图,
设KH的中点为S,连接PE,PF,SE,SF,PS,
∵E为MN的中点,S为KH的中点,
∴A,E,S共线,
F为QR的中点,S为KH的中点,
∴B、F、S共线,
由△AME∽△PQF,得∠SAP=∠FPB,
∴ES∥PF,
△PNE∽△BRF,得∠EPA=∠FBP,
∴PE∥FS,
则四边形PESF为平行四边形,则G为PS的中点,
∴G的轨迹为△CSD的中位线,
∵CD=AB-AC-BD=6-1-1=4,
∴点G移动的路径长$\frac{1}{2}×4=2$.
故答案为:2.
点评 本题考查了轨迹方程,考查了三角形的中位线知识,考查了三角形相似及动点的轨迹,是中档题.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:解答题
 如图,方格纸中的每个小方格都是边长为1个单位的正方形,Rt△ABC的顶点均在格点上,在建立平面直角坐标系后,点A的坐标为(-7,1),点B的坐标为(-3,1),点C的坐标为(-3,3).
如图,方格纸中的每个小方格都是边长为1个单位的正方形,Rt△ABC的顶点均在格点上,在建立平面直角坐标系后,点A的坐标为(-7,1),点B的坐标为(-3,1),点C的坐标为(-3,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0)C(8,0)D(8,8)抛物线y=ax2+bx过A,C两点,动点P从点A出发,沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD向终点D运动,速度均为每秒1个单位长度,运动时间为t秒,过点P作PE⊥AB交AC于点E
如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0)C(8,0)D(8,8)抛物线y=ax2+bx过A,C两点,动点P从点A出发,沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD向终点D运动,速度均为每秒1个单位长度,运动时间为t秒,过点P作PE⊥AB交AC于点E查看答案和解析>>
科目:初中数学 来源: 题型:选择题
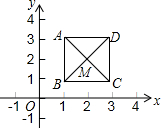 如图,已知正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1).规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换.如此这样,连续经过2015次变换后,正方形ABCD的对角线交点M的坐标变为( )
如图,已知正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1).规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换.如此这样,连续经过2015次变换后,正方形ABCD的对角线交点M的坐标变为( )| A. | (-2013,2) | B. | (-2013,-2) | C. | (-2014,-2) | D. | (-2014,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com