

分析 (1)欲证明AB=BC,只要证明∠A=∠C即可.
(2)欲证明EF=BE+CF,只要证明EO=EB,FO=FC即可.
(3)欲证明EF=BE-CF,只要证明EO=EB,FO=FC即可.
解答 证明:(1)如图1中,∵DE∥BC,
∴∠EDB=∠DBC,∠ADE=∠C
∵BD平分∠EBC,
∴∠DBC=∠DBE,
∴∠EDB=∠EBD,
∴EB=ED,∵AE=BE,
∴EA=ED,
∴∠A=∠EDA,
∴∠A=∠C,
∴BA=BC.
(2)如图2中,∵EF∥BC,
∴∠EOB=∠2,∠FOC=∠3,
∵∠1=∠2,∠3=∠4,
∴∠1=∠EOB,∠4=∠FOC,
∴EO=EB,FO=FC,
∴EF=EO+OF=EB+CF.
(3)如图3中,∵EF∥BC,
∴∠EOB=∠2,∠FOC=∠3,
∵∠1=∠2,∠3=∠4,
∴∠1=∠EOB,∠4=∠FOC,
∴EO=EB,FO=FC,
∴EF=EO-OF=EB-CF.
点评 本题考查等腰三角形的判定和性质、平行线的性质等知识,解题的关键是灵活运用等腰三角形的判定解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
| A. | M=N | B. | M<N | C. | M>N | D. | 无法比较 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
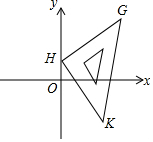 课间,顽皮的小刚拿着老师的等腰直角三角板放在黑板上画好了的平面直角坐标系内(如图),已知直角顶点H的坐标为(0,1),另一个顶点G的坐标为(4,4),则点K的坐标为(3,-3).
课间,顽皮的小刚拿着老师的等腰直角三角板放在黑板上画好了的平面直角坐标系内(如图),已知直角顶点H的坐标为(0,1),另一个顶点G的坐标为(4,4),则点K的坐标为(3,-3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,已知△ABC中,∠C=90°,AB=5cm,AC=3cm,BC=4cm,AD是∠CAB的平分线,与BC交于D,DE⊥AB于E,则
如图所示,已知△ABC中,∠C=90°,AB=5cm,AC=3cm,BC=4cm,AD是∠CAB的平分线,与BC交于D,DE⊥AB于E,则查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com