练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在抛物线y＝x2－4x－4上的一个点是（ ）

    A.（4，4）B.（3，－1）C.（－2，－8）D.（－1，1）

    【答案】D

    【解析】

    先分别计算当自变量为4、3、-2、-1时，所对应的函数值，然后根据二次函数图象上点的坐标满足其解析式进行判断即可；

    解：选项A中，当x=4时，y＝x2－4x－4＝4，点（4，4）不在抛物线上，故选项A错误；

    选项B中，当x=3时，y＝x2－4x－4=7，点（3，-1）不在抛物线上，故选项B错误；

    选项C中，当x=2时，y＝x2－4x－4=8，点（-2，-8）不在抛物线上，故选项C错误；

    选项D中，当x=1时，y＝x2－4x－4=1，点（-1，1）在抛物线上，故选项D正确；

    故选D.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】三角形的内角分别为55°和65°，下列四个角中，不可能是这个三角形外角的是（ ）

    A. 115° B. 120° C. 125° D. 130°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】A市和B市分别有库存的某联合收割机12台和6台，现决定开往C市10台和D市8台，已知从A市开往C市、D市的油料费分别为每台400元和800元，从B市开往C市和D市的油料费分别为每台300元和500元．
    （1）设B市运往C市的联合收割机为x台，求运费w关于x的函数关系式．
    （2）若总运费不超过9000元，问有几种调运方案？
    （3）求出总运费最低的调运方案，并求出最低运费．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知正方形，点为边的中点.

    （1）如图1，点为线段上的一点，且，延长，分别与边，交于点，.

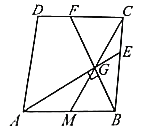
    ①求证：；

    ②求证：.

    （2）如图2，在边上取一点，满足，连接交于点，连接延长交于点，求的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】平行四边形ABCD中，∠ABC的平分线将AD边分成的两部分的长分别为2和3，则平行四边形ABCD的周长是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】自2016年国庆后，许多高校均投放了使用手机就可随用的共享单车．某运营商为提高其经营的A品牌共享单车的市场占有率，准备对收费作如下调整：一天中，同一个人第一次使用的车费按0.5元收取，每增加一次，当次车费就比上次车费减少0.1元，第6次开始，当次用车免费．具体收费标准如下：

    使用次数

    0

    1

    2

    3

    4

    5(含5次以上)

    累计车费

    0

    0.5

    0.9

    1.5

    同时，就此收费方案随机调查了某高校100名师生在一天中使用A品牌共享单车的意愿，得到如下数据：

    使用次数

    0

    1

    2

    3

    4

    5

    人数

    5

    15

    10

    30

    25

    15

    （Ⅰ）写出的值；

    （Ⅱ）已知该校有5000名师生，且A品牌共享单车投放该校一天的费用为5800元．试估计：收费调整后，此运营商在该校投放A品牌共享单车能否获利? 说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明和他爸爸做了一个实验，小明由一幢245米高的楼顶随手放下一只苹果，由他爸爸测量有关数据，得到苹果下落的路程和下落的时间之间有下面的关系：

    下落时间t（s）

    1

    2

    3

    4

    5

    6

    下落路程s（m）

    5

    20

    45

    80

    125

    180

    下列说法错误的是（　　）

    A.苹果每秒下落的路程不变B.苹果每秒下落的路程越来越长

    C.苹果下落的速度越来越快D.可以推测，苹果下落7秒后到达地面

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】中国倡导的“一带一路”建设将促进我国与世界各国的互利合作，根据规划，“一带一路”地区覆盖总人口约为4400000000人，这个数用科学记数法表示为（　　）

    A.44×108B.4.4×109C.4.4×108D.4.4×1010

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：甲乙两车分别从相距300千米的A、B两地同时出发相向而行，其中甲到达B地后立即返回，如图是它们离各自出发地的距离y（千米）与行驶时间x（小时）之间的函数图象．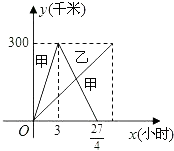
    （1）求甲车离出发地的距离y甲（千米）与行驶时间x（小时）之间的函数关系式，并写出自变量的取值范围；
    （2）它们出发 小时时，离各自出发地的距离相等，求乙车离出发地的距离y乙（千米）与行驶时间x（小时）之间的函数关系式，并写出自变量的取值范围；
    （3）在（2）的条件下，求它们在行驶的过程中相遇的时间．

    查看答案和解析>>

    同步练习册答案