
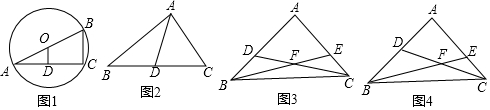
���� ��1������������λ�߶����ɵ�OD=$\frac{1}{2}$BC���ɴ˼��ɽ�����⣻
��2����ͼ2�У��ӳ�AD��M��ʹ��DM=AD������BM��CM���ڡ�ABM�У��������߹�ϵ�����ɵ�6-4��AM��6+4����2��2AD��10��1��AD��5��
��3���ٽ��ۣ�EF=CE����ͼ4�У��ӳ�CD��Mʹ��DM=CD������BM���ɡ�ADC�ա�BDM���Ƴ�BM=AC����M=��ACD����BM��AC���Ƴ���CEF�ס�MBF��
�ɵ�$\frac{EF}{BF}$=$\frac{CE}{BM}$���Ƴ�$\frac{EF}{BF}$=$\frac{CE}{AC}$=$\frac{1}{m}$���Ƴ�BF=mEF���Ƴ�BE=��m+1��EF����Rt��BAE�У�BE=$\sqrt{A{B}^{2}+A{E}^{2}}$=$\sqrt{��2\sqrt{m}EC��^{2}+[��m+1��EC]^{2}}$=��m+1��EC���Ƴ���m+1��EC=��m+1��EF���ɴ˼���֤����
���ۣ�$\frac{CE}{EF}$=$\frac{m+n}{n��m+1��}$����ͼ3�У���BM��AC��CD���ӳ�����M��֤���������Ƣ٣�
��� �⣺��1����ͼ1�У�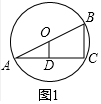
��OD��AC��
��AD=DC��
��AO=OB��BC=6��
��OD=$\frac{1}{2}$BC=3��
��2����ͼ2�У��ӳ�AD��M��ʹ��DM=AD������BM��CM��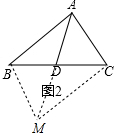
��AD=DM��BD=CD��
���ı���ABMC��ƽ���ı��Σ�
��BM=AC=4����AB=6��
��6-4��AM��6+4��
��2��2AD��10��
��1��AD��5��
��3���ٽ��ۣ�EF=CE��
���ɣ���ͼ4�У��ӳ�CD��Mʹ��DM=CD������BM��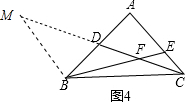
��AD=DB����ADC=��BDM��
���ADC�ա�BDM��
��BM=AC����M=��ACD��
��BM��AC��
���CEF�ס�MBF��
��$\frac{EF}{BF}$=$\frac{CE}{BM}$��
��$\frac{EF}{BF}$=$\frac{CE}{AC}$=$\frac{1}{m}$��
��BF=mEF��
��BE=��m+1��EF��
��Rt��BAE��BE=$\sqrt{A{B}^{2}+A{E}^{2}}$=$\sqrt{��2\sqrt{m}EC��^{2}+[��m+1��EC]^{2}}$=��m+1��EC��
�ࣨm+1��EC=��m+1��EF��
��EF=CE��
�ڽ��ۣ�$\frac{CE}{EF}$=$\frac{m+n}{n��m+1��}$��
���ɣ���ͼ3�У���BM��AC��CD���ӳ�����M��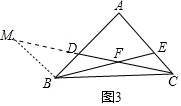
�ɡ�ADC�ס�BDM���ɵ�$\frac{AD}{BD}$=$\frac{AC}{MB}$=n��
��BM=$\frac{AC}{n}$��
��$\frac{EC}{BM}$=$\frac{EF}{BF}$��
��$\frac{EC}{\frac{AC}{n}}$=$\frac{EF}{BF}$��
��AC=mEC��
��BF=$\frac{m}{n}$EF��
��BE=��1+$\frac{m}{n}$��EF��
��Rt��BAE��BE=$\sqrt{A{B}^{2}+A{E}^{2}}$=$\sqrt{��2\sqrt{m}EC��^{2}+[��m+1��EC]^{2}}$=��m+1��EC��
�ࣨm+1��EC=��1+$\frac{m}{n}$��EF��
��$\frac{EC}{EF}$=$\frac{m+n}{n��m+1��}$��
���� ���⿼��Բ�ۺ��⡢����������ȫ�������ε��ж������ʡ����������ε��ж������ʡ����ɶ�����֪ʶ������Ĺؼ���ѧ�����ӳ��ø����ߣ�����ȫ�������λ����������ν�����⣬�����п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{2}$ | B�� | $\sqrt{\frac{1}{8}}$ | C�� | $\sqrt{0.2}$ | D�� | $\sqrt{27}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
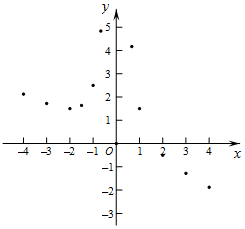 ������һ�����⣺̽������y=$\frac{2}{{x}^{2}}$-$\frac{1}{2}$x��ͼ�������ʣ�
������һ�����⣺̽������y=$\frac{2}{{x}^{2}}$-$\frac{1}{2}$x��ͼ�������ʣ�| x | �� | -4 | -3 | -2 | -$\frac{3}{2}$ | -1 | -$\frac{2}{3}$ | $\frac{2}{3}$ | 1 | 2 | 3 | 4 | �� |
| y | �� | $\frac{17}{8}$ | $\frac{31}{18}$ | $\frac{3}{2}$ | $\frac{59}{36}$ | $\frac{5}{2}$ | $\frac{29}{6}$ | $\frac{25}{6}$ | $\frac{3}{2}$ | -$\frac{1}{2}$ | -$\frac{23}{18}$ | m | �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a+1 | B�� | a-1 | C�� | -a-1 | D�� | -a+1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3x-2x=1 | B�� | ��-a3��2=-a6 | C�� | x6��x2=x3 | D�� | x3•x2=x5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com