
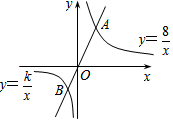
 如图,点A为反比例函数y=$\frac{8}{x}$(x>0)图象上一点,点B为反比例函数y=$\frac{k}{x}$
如图,点A为反比例函数y=$\frac{8}{x}$(x>0)图象上一点,点B为反比例函数y=$\frac{k}{x}$| A. | 2 | B. | 4 | C. | -2 | D. | -4 |
分析 过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,由反比例函数系数k的几何意义可得出S△AOC=4,再由相似三角形的判定定理得出△AOC∽△BOD,由相似三角形的性质可得出△BOD的面积,进而可得出结论.
解答 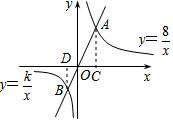 解:过点A作AC⊥x轴于点D,过点B作BD⊥x轴于点D,
解:过点A作AC⊥x轴于点D,过点B作BD⊥x轴于点D,
∵点A为反比例函数y=$\frac{8}{x}$(x>0)图象上一点,
∴S△AOC=$\frac{1}{2}$×8=4.
∵AC⊥x轴,BD⊥x轴,
∴∠OBD=∠OAC.
∵∠BOD=∠AOC,
∴△AOC∽△BOD.
∵OA=2OB,S△AOC=4,
∴$\frac{{S}_{△BOD}}{{S}_{△AOC}}$=$\frac{1}{4}$,
∴S△BOD=1,
∵S△BOD=$\frac{1}{2}$|k|,
∴k=2.
故选A.
点评 本题考查的是反比例函数系数k的几何意义,根据题意作出辅助线,构造出相似三角形是解答此题的关键.


 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:填空题
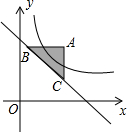 如图,在平面直角坐标系中,过点A(4,5)分别作x轴、y轴的平行线,交直线y=-x+6于B、C两点.若函数y=$\frac{k}{x}$(x>0)的图象与△ABC的边有公共点,则k的取值范围是5≤k≤20.
如图,在平面直角坐标系中,过点A(4,5)分别作x轴、y轴的平行线,交直线y=-x+6于B、C两点.若函数y=$\frac{k}{x}$(x>0)的图象与△ABC的边有公共点,则k的取值范围是5≤k≤20.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
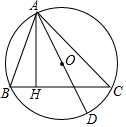 如图,AD是△ABC的外接圆O的直径,AH⊥BC于H.
如图,AD是△ABC的外接圆O的直径,AH⊥BC于H.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
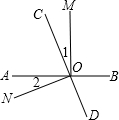 如图,直线AB、CD相交于点O,OM⊥AB.
如图,直线AB、CD相交于点O,OM⊥AB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
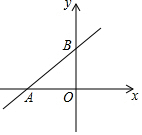 如图,直线y=kx+b与x轴、y轴分别相交于点A(-3,0)、B(0,2),则不等式kx+b>0的解集是( )
如图,直线y=kx+b与x轴、y轴分别相交于点A(-3,0)、B(0,2),则不等式kx+b>0的解集是( )| A. | x>-3 | B. | x<-3 | C. | x>2 | D. | x<2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,称为第1次操作,折痕DE到BC的距离记为h1,还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕D1E1到BC的距离记为h2;按上述方法不断操作下去…,经过第2017次操作后得到的折痕D2016E2016,到BC的距离记为h2017;若h1=1,则h2017的值为2-$\frac{1}{{2}^{2016}}$.
如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,称为第1次操作,折痕DE到BC的距离记为h1,还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕D1E1到BC的距离记为h2;按上述方法不断操作下去…,经过第2017次操作后得到的折痕D2016E2016,到BC的距离记为h2017;若h1=1,则h2017的值为2-$\frac{1}{{2}^{2016}}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com