
【题目】如图,正方形 ABCD 中,点 G 是边 CD 上一点(不与端点 C,D 重合),以 CG为边在正方形 ABCD 外作正方形 CEFG,且 B、C、E 三点在同一直线上,设正方形 ABCD 和正方形 CEFG 的边长分别为 a 和 b.
(1)分别用含 a,b 的代数式表示图 1 和图 2 中阴影部分的面积 S1、S2;
(2)如果 a+b=5,ab=3,求 S1 的值;
(3)当 S1<S2 时,求![]() 的取值范围.
的取值范围.

【答案】(1)S1= ![]() a2+
a2+ ![]() b2﹣
b2﹣![]() ab, S2=ab﹣
ab, S2=ab﹣![]() b2;(2)8;(3)1<
b2;(2)8;(3)1<![]() <2.
<2.
【解析】(1)利用两个正方形的面积减去空白部分的面积列式即可;
(2)把a+b=5,ab=3,整体代入S1的代数式求得数值即可;
(3)联立不等式,进一步求得答案即可.
(1)S1=a2+b2-![]() a2-
a2-![]() b(a+b)
b(a+b)
=![]() a2+
a2+![]() b2-
b2-![]() ab,
ab,
S2=a(a+b)-b2-![]() a2-
a2-![]() (a-b)(a+b)
(a-b)(a+b)
=ab-![]() b2.
b2.
(2)∵a+b=5,ab=3,
∴S1=![]() a2+
a2+![]() b2-
b2-![]() ab
ab
=![]() (a+b)2-
(a+b)2-![]() ab=
ab=![]() .
.
(3)∵![]() a2+
a2+![]() b2-
b2-![]() ab<ab-
ab<ab-![]() b2.
b2.
∴![]() a2+b2-
a2+b2-![]() ab<0,
ab<0,
∴a2+2b2-3ab<0,
∴(a-2b)(a-b)<0,
∵a>b,
∴a-2b<0,
∴a<2b,
∴1<![]() <2.
<2.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,与反比例函数y= ![]() 的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO=
的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO= ![]() ,OB=4,OE=2.
,OB=4,OE=2. 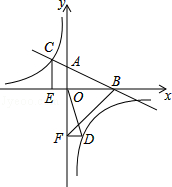
(1)求反比例函数的解析式;
(2)若点D是反比例函数图象在第四象限上的点,过点D作DF⊥y轴,垂足为点F,连接OD、BF.如果S△BAF=4S△DFO , 求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当今社会手机越来越普及,有很多人开始过份依赖手机,一天中使用手机时间过长而形成了“手机瘾”.为了解我校初三年级学生的手机使用情况,学生会随机调查了部分学生的手机使用时间,将调查结果分成五类:A、基本不用;B、平均一天使用1~2小时;C、平均一天使用2~4小时;D、平均一天使用4~6小时;E、平均一天使用超过6小时.并用得到的数据绘制成了如下两幅不完整的统计图(图1、2),请根据相关信息,解答下列问题: 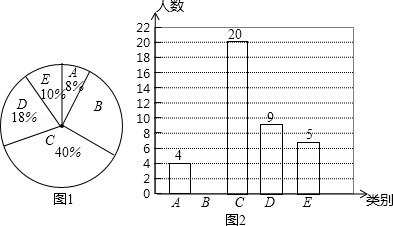
(1)将上面的条形统计图补充完整;
(2)若一天中手机使用时间超过6小时,则患有严重的“手机瘾”.我校初三年级共有1490人,试估计我校初三年级中约有多少人患有严重的“手机瘾”;
(3)在被调查的基本不用手机的4位同学中有2男2女,现要从中随机再抽两名同学去参加座谈,请你用列表法或树状图方法求出所选两位同学恰好是一名男同学和一位女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,关于 x,y 的方程组![]() 的解满足 x<0,y>0.
的解满足 x<0,y>0.
(1)x= ,y= (用含 a 的代数式表示);
(2)求 a 的取值范围;
(3)若 2x8y=2m,用含有 a 的代数式表示 m,并求 m 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
组别 | 成绩x分 | 频数(人数) |
第1组 | 50≤x<60 | 6 |
第2组 | 60≤x<70 | 8 |
第3组 | 70≤x<80 | 14 |
第4组 | 80≤x<90 | a |
第5组 | 90≤x<100 | 10 |
请结合图表完成下列各题:
(1)①表中a的值为; ②频数分布直方图补充完整;
(2)若测试成绩不低于80分为优秀,则本次测试的优秀率是 .
(3)第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小明与小强两名男同学能分在同一组的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD和矩形PEFG中,AB=8,BC=6,PE=2,PG=4.PE与AC交于点M,EF与AC交于点N,动点P从点A出发沿AB以每秒1个单位长的速度向点B匀速运动,伴随点P的运动,矩形PEFG在射线AB上滑动;动点K从点P出发沿折线PE﹣﹣EF以每秒1个单位长的速度匀速运动.点P、K同时开始运动,当点K到达点F时停止运动,点P也随之停止.设点P、K运动的时间是t秒(t>0). 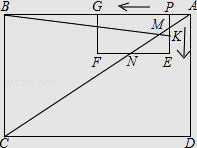
(1)当t=1时,KE= , EN=;
(2)当t为何值时,△APM的面积与△MNE的面积相等?
(3)当点K到达点N时,求出t的值;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班师生组织植树活动,上午8时从学校出发,到植树地点后原路返校,如图为师生离校路程s与时间t之间的图象,请回答下列问题:
![]() 试写出师生返校时的s与t的函数关系式,并求出师生何时回到学校;
试写出师生返校时的s与t的函数关系式,并求出师生何时回到学校;
![]() 如果师生骑自行车上午8时出发,到植树地点后,植树需2小时,要求14时前返回到学校,往返平均速度分别为每时10km、8km,现有A、B、C、D四个植树点与学校的路程分别是13km、15km、17km、19km,试通过计算说明哪几个植树点符合要求.
如果师生骑自行车上午8时出发,到植树地点后,植树需2小时,要求14时前返回到学校,往返平均速度分别为每时10km、8km,现有A、B、C、D四个植树点与学校的路程分别是13km、15km、17km、19km,试通过计算说明哪几个植树点符合要求.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司试销一种成本为30元/件的新产品,按规定试销时的销售单价不低于成本单价,又不高于80元/件,试销中每天的销售量y(件)与销售单价x(元/件)满足下表中的函数关系.
(1)试求y与x之间的函数表达式;(2)设公司试销该产品每天获得的毛利润为S(元),求S与x之间的函数表达式(毛利润=销售总价-成本总价);
(2)当销售单价定为多少时,该公司试销这种产品每天获得的毛利润最大?
(3)最大毛利润是多少?此时每天的销售量是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com