

分析 (1)先求出∠EAC,再根据∠BAE=∠BAC+∠EAC即可解决问题.
(2)根据角的和差定义即可证明.
(3)根据两个变量和为定值,其中一个变量变大,另一个变量变小,即可解决.
(4)如图乙中,作EO⊥ON,FO⊥OM,则∠EOF=∠MON,根据角的和差定义即可证明.
解答 解:(1)∵∠DAE=70°20′,∠DAC=27°20′,
∴∠CAE=∠DAE-∠DAC=70°20′-27°20′=43°,
∴∠BAE=∠BAC+∠CAE=70°20′+43°=113°20′.
故答案为113°20′.
(2)∵∠BAC=∠BAE,
∴∠BAD+∠DAC=∠EAC+∠DAC,
∴∠BAD=∠EAC,
故答案为∠EAC.
(3)∵∠DAC+∠DAB=70°20′,
∴若∠DAC变大,∠DAB变小.
故答案为变小.
(4)如图乙中,使得∠EOM=∠FOM=90°(使用了三角板中的90度角),则∠EOF=∠MON.
理由:∵∠EON=∠FOM=90°,
∴∠EOF=∠FOM-∠EOM,∠MON=∠EON-∠EOM,
∴∠EOF=∠MON.
点评 本题考查角的和差定义,度、分、秒换算等知识,解题的关键是灵活应用这些知识解决问题,属于基础题,中考常考题型.


科目:初中数学 来源: 题型:解答题
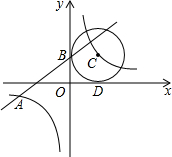 如图,已知一次函数y1=kx+b的图象与反比例函数y2=$\frac{4}{x}$的图象交于点A(-4,m),且与y轴交于点B,第一象限内点C在反比例函数y2=$\frac{4}{x}$的图象上,且以点C为圆心的圆与x轴,y轴分别相切于点D,B
如图,已知一次函数y1=kx+b的图象与反比例函数y2=$\frac{4}{x}$的图象交于点A(-4,m),且与y轴交于点B,第一象限内点C在反比例函数y2=$\frac{4}{x}$的图象上,且以点C为圆心的圆与x轴,y轴分别相切于点D,B查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知不等式组$\left\{\begin{array}{l}{x≥-a-1}&{①}\\{-x≥-b}&{②}\end{array}\right.$,在同一条数轴上表示不等式①,②的解集如图所示,则b-a的值为$\frac{1}{3}$.
已知不等式组$\left\{\begin{array}{l}{x≥-a-1}&{①}\\{-x≥-b}&{②}\end{array}\right.$,在同一条数轴上表示不等式①,②的解集如图所示,则b-a的值为$\frac{1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠BAC=90°,AB=4,AC=3,点D为BC的中点,动点P从点A出发,以每秒1个单位长度的速度沿线段AB向点B运动,当点P离开点A后,过点P作PE⊥AB交BC于点E,过点E作EF⊥AC于F,设点P运动时间为t(秒),矩形PEFA与△ADE重叠部分的面积为S平方单位长度.
如图,在Rt△ABC中,∠BAC=90°,AB=4,AC=3,点D为BC的中点,动点P从点A出发,以每秒1个单位长度的速度沿线段AB向点B运动,当点P离开点A后,过点P作PE⊥AB交BC于点E,过点E作EF⊥AC于F,设点P运动时间为t(秒),矩形PEFA与△ADE重叠部分的面积为S平方单位长度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
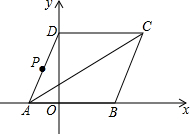 如图所示,菱形ABCD的顶点A、B在x轴上,点A在点B的左侧,点D在y轴的正半轴上,∠BAD=60°.点A的坐标为(-2,0).
如图所示,菱形ABCD的顶点A、B在x轴上,点A在点B的左侧,点D在y轴的正半轴上,∠BAD=60°.点A的坐标为(-2,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com