练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．将一张矩形纸片ABCD沿直线MN折叠，使点C落在点A处，点D落在点E处，直线MN交BC于点M，交AD于点N，若AB=4，AD=8，则线段AN的长为（　　）
    A．8B．12C．5D．4

    分析 由折叠得到AM=CM，设CM=x，则BM=8-x，关键勾股定理求出x，再判断四边形AMCN是平行四边形，即可．

    解答 解：在矩形纸片ABCD中，AB=4，AD=8，
    ∴∠B=∠D，AD∥BC，BC=8，
    由折叠得，AM=CM，
    设CM=x，则BM=8-x，
    在RT△ABM中，AM2=AB2+BM2，
    即x2=16+（8-x）2，
    ∴x=5，
    ∴CM=5，
    由折叠得，AM∥NC，
    ∵AD∥BC，
    ∴四边形AMCN是平行四边形，
    ∴AN=CM=5，
    故选C，

    点评 此题是折叠问题，考查了矩形的性质、折叠的性质、勾股定理以及平行四边形的性质和判定．用勾股定理求出CM是解本题的关键；此题难度适中，掌握数形结合思想与方程思想的应用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    7．已知四边形ABCD的面积为20cm2，将该四边形向右平移一定距离后得到新的四边形EFGH，则四边形EFGH的面积为20cm2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．如图，在正方形ABCD中，点E、F分别在BC、CD上，且BE=DF，若∠EAF=30°，则sin∠EDF=$\frac{（\sqrt{3}-1）\sqrt{7+2\sqrt{3}}}{\sqrt{37}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

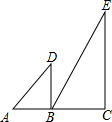    5．如图，在直线AC的同侧有Rt△ABD和Rt△BCE，已知∠ABD=∠C=90°，∠A=45°，∠E=30°，若将△ABD绕点B按顺时针方向旋转，当AD∥BC时，旋转的角度是（　　）
    A．30°B．45°C．60°D．90°

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

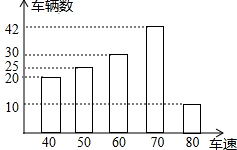    12．为了解一段路车辆行驶速度的情况，交警统计了该路段上午7：00至9：00来往车辆的车速（（单位：千米/时），并绘制成如图所示的条形统计图，这些车速的众数、中位数分别是（　　）
    A．80，60B．70，70C．60，60D．70，60

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．代数式$\sqrt{1-x}$有意义，则x的取值范围是（　　）
    A．x＞1，且x≠0B．x≥1C．x≠1D．x≤1

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．如图，在?ABCD中，BE平分∠ABC，BC=6，DE=2，则?ABCD的周长等于（　　）
    A．20B．18C．16D．14

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．在平面直角坐标系中，有A（3，2），B （-1，-4 ），P是x轴上的一点，Q是y轴上的一点，若以点A，B，P，Q四个点为顶点的四边形是平行四边形，请写出Q点的坐标（0，-6）或（0，-2）或（0，6） ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．下列四个水平放置的几何体中，三视图如图所示的是（　　）
    A．
    立方体    		B．
    三棱柱    		C．
    圆柱    		D．
    长方体

    查看答案和解析>>

    同步练习册答案