
【题目】如图1, ![]() 与
与 ![]() 为等腰直角三角形,
为等腰直角三角形, ![]() 与
与 ![]() 重合,
重合, ![]() ,
, ![]() .固定
.固定 ![]() ,将
,将 ![]() 绕点
绕点 ![]() 顺时针旋转,当
顺时针旋转,当 ![]() 边与
边与 ![]() 边重合时,旋转终止.现不考虑旋转开始和结束时重合的情况,设
边重合时,旋转终止.现不考虑旋转开始和结束时重合的情况,设 ![]() (或它们的延长线)分别交
(或它们的延长线)分别交 ![]() (或它们的延长线)于点
(或它们的延长线)于点 ![]() ,如图2.
,如图2.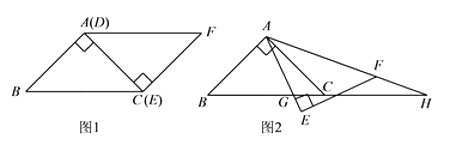
(1)证明: ![]() ;
;
(2)当 ![]() 为何值时,
为何值时, ![]() 是等腰三角形?
是等腰三角形?
【答案】
(1)证明:∵△ABC与△EFD为等腰直角三角形,AC与DE重合,
∴∠B=∠EDF=45°
在△AGC和△HAB中
∵∠ACG=∠B=45°,
∠HAB=∠BAG+∠GAH =∠BAG+45°=∠CGA
∴△AGC∽△HAB
(2)解:①当∠GAH=45是等腰三角形的底角时,
如图可知: ![]() ;
;

②当∠GAH=45是等腰三角形的顶角时,如图:

在△HGA和△AGC中,
∵∠AGH=∠CGA,∠GAH=∠C=45,
∴△HGA∽△AGC,∵AG=AH,
∴ ![]()
③如图,G与B重合时,符合要求,

此时CG=BC= ![]()
∴当 ![]() 或
或 ![]() 或
或 ![]() 时,
时,
△AGH是等腰三角形
【解析】第1小题,根据等腰三角形的性质可得∠B=∠EDF=45°,由有两个角对应相等的两个三角形相似可证△AGC∽△HAB;第2小题,分三种情况,①当∠GAH=45是等腰三角形的底角时;②当∠GAH=45是等腰三角形的顶角时;③G与B重合时。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,从下列四个条件①AB=BC,②AC⊥BD,③∠ABC=90°,④AC=BD中选两个作为补充条件,使ABCD成为正方形,下列四种选法错误的是( )
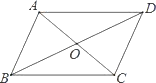
A. ①②B. ①③C. ②③D. ①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连结EF、EO,若DE= ![]() ,∠DPA=45°.
,∠DPA=45°.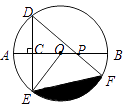
(1)求⊙O的半径;
(2)求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的面积为12,△ABC是等边三角形,点E在正方形ABCD内,对角线AC上有一点P使PE+PD的和最小,这个最小值为( )

A. ![]() B.
B. ![]() C. 3 D.
C. 3 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的.连接BE、CF相交于点D.
(1)求证:BE=CF.
(2)当四边形ACDE为菱形时,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M,N.当∠MAN绕点A旋转到BM=DN时(如图1),易证BM+DN=MN.

(1)当∠MAN绕点A旋转到BM≠DN时(如图2),线段BM,DN和MN之间有怎样的数量关系?写出猜想,并加以证明.
(2)当∠MAN绕点A旋转到如图3的位置时,线段BM,DN和MN之间又有怎样的数量关系?请直接写出你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(三角形顶点是网格线的交点)和△A1B1C1 , △ABC与△A1B1C1成中心对称.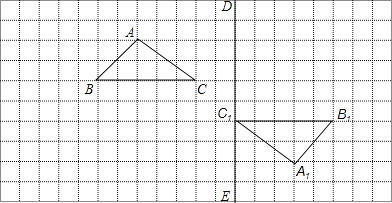
(1)画出△ABC和△A1B1C1的对称中心O;
(2)将△A1B1C1 , 沿直线ED方向向上平移6格,画出△A2B2C2;:
(3)将△A2B2C2绕点C2顺时针方向旋转90°,画出△A3B3C3 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】晓琳和爸爸到太子河公园运动,两人同时从家出发,沿相同路线前行,途中爸爸有事返回,晓琳继续前行5分钟后也原路返回,两人恰好同时到家.晓琳和爸爸在整个运动过程中离家的路程y1(米),y2(米)与运动时间x(分)之间的函数关系如图所示,下列结论:①两人同行过程中的速度为200米/分;②m的值是15,n的值是3000;③晓琳开始返回时与爸爸相距1800米;④运动18分钟或30分钟时,两人相距900米.其中正确结论的个数是( )
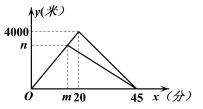
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com