
【题目】某中学举行演讲比赛,七年级(1)班、(2)班根据初赛成绩各选出5名选手参加复赛,两个班所选出的5名选手的复赛成绩如下面条形统计图所示.
平均分(分) | 中位数(分) | 众数(分) | 方差 | |
(1)班 | 85 | a | 85 | 70 |
(2)班 | 85 | 80 | b | c |
(1)根据条形统计图中的信息,求上表中a,b,c的值;
(2)请你分析说明哪个班级的复赛成绩较好.

【答案】(1)表格中的a的值为85,b的值为100,c的值为160;(2)一班的成绩的方差较小,比较稳定,但高分较少,而二班虽然中位数较小,方差较大,但高分人数较多,从优秀人数看,二班的成绩较好.
【解析】
(1)从统计图中得出两个班的成绩,将(1)班的成绩排序后找出处在第3位的数即为中位数,找(2)班成绩中出现次数最多的数就是众数,计算出(2)班的平均数,再利用方差计算公式进行计算可得c的值;
(2)从中位数、众数、方差等方面分析得出答案.
解:(1)(1)班的中位数是85分,(2)班的众数是100分,
(2)班的平均数为:(70+75+80+100+100)÷5=85分,
(2)班的方差为:S2=![]() [(70-85)2+(75-85)2+(80-85)2+(100-85)2+(100-85)2]=160,
[(70-85)2+(75-85)2+(80-85)2+(100-85)2+(100-85)2]=160,
答:表格中的a的值为85,b的值为100,c的值为160.
(2)(1)班的成绩的方差较小,比较稳定,但高分较少,而(2)班虽然中位数较小,方差较大,但高分人数较多,从优秀人数看,(2)班的成绩较好.
故答案为:(1)表格中的a的值为85,b的值为100,c的值为160;(2)(1)班的成绩的方差较小,比较稳定,但高分较少,而(2)班虽然中位数较小,方差较大,但高分人数较多,从优秀人数看,(2)班的成绩较好.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
【题目】我市建设森林城市需要大量的树苗,某生态示范园负责对甲、乙、丙、丁四个品种的树苗共500株进行树苗成活率试验,从中选择成活率高的品种进行推广.通过试验得知:丙种树苗的成活率为89.6%,把试验数据绘制成下面两幅统计图.(部分信息未给出)
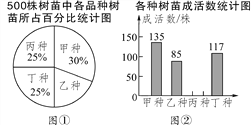
(1)试验所用的乙种树苗的数量是_______株;
(2)求出丙种树苗的成活数,并把图②补充完整;
(3)你认为应选哪种树苗进行推广?请通过计算说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学统计了家中10月份的长途电话清单,并按通话时间画出了如图所示的统计图(每组数据含左端点值,不含右端点值).
(1)该同学家这个月一共打了多少次长途电话?
(2)通话时间不足10分钟的有多少次?
(3)哪个时间范围内的通话次数最多?哪个时间范围内的通话次数最少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
, ![]() 是一次函数
是一次函数![]() 的图象和反比例函数
的图象和反比例函数![]() 的图象的两个交点.
的图象的两个交点.
(1) 求一次函数、反比例函数的关系式;
(2) 求△AOB的面积.
(3) 当自变量x满足什么条件时,y1>y2 .(直接写出答案)
(4)将反比例函数![]() 的图象向右平移n(n>0)个单位,得到的新图象经过点(3,-4),求对应的函数关系式y3.(直接写出答案)
的图象向右平移n(n>0)个单位,得到的新图象经过点(3,-4),求对应的函数关系式y3.(直接写出答案)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】分解因式x2-4y2-2x+4y,细心观察这个式子就会发现,前两项符合平方差公式,后两项可提取公因式,前后两部分分别分解因式后会产生公因式,然后提取公因式就可以完成整个式子的分解因式,过程为:x2-4y2-2x+4y=(x+2y)(x-2y)-2(x-2y)=(x-2y)(x+2y-2).这种分解因式的方法叫分组分解法,利用这种方法解决下列问题:
(1)分解因式:a2-4a-b2+4;
(2)若△ABC三边a、b、c满足a2-ab-ac+bc=0,试判断△ABC的形状.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点A(-2,2),B(0,5),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,得到△A1B1C,请画出△A1B1C的图形.
(2)平移△ABC,使点A的对应点A2坐标为(-2,-6),请画出平移后对应的△A2B2C2的图形.
(3)若将△A1B1C绕某一点旋转可得到△A2B2C2,请直接写出旋转中心的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC⊥x轴于点A,点B在y轴的正半轴上,∠ABC=60°,AB=4,BC=![]() ,点D为AC与反比例函数
,点D为AC与反比例函数![]() 的图象的交点.若直线BD将△ABC的面积分成1:2的两部分,则k的值为______.
的图象的交点.若直线BD将△ABC的面积分成1:2的两部分,则k的值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
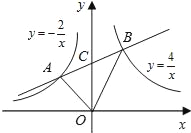
【题目】如图,点A是反比例函数![]() 在第二象限内图象上一点,点B是反比例函
在第二象限内图象上一点,点B是反比例函![]() 数在第一象限内图象上一点,直线AB与y轴交于点C,且AC=BC,连接OA、OB,求△AOB的面积.
数在第一象限内图象上一点,直线AB与y轴交于点C,且AC=BC,连接OA、OB,求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
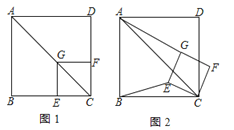
【题目】如图,已知点G在正方形ABCD的对角线AC上,GE⊥BC,GF⊥CD,垂足分别为点E,F.
(1)求证:四边形CEGF是正方形;
(2)将正方形CEGF绕点C顺时针旋转![]() ,如图所示,线段BE与DF是否相等?为什么?
,如图所示,线段BE与DF是否相等?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com