练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】点（-4，5）到x轴上的距离是_______，到y轴上的距离是_______。

    【答案】5 ；4

    【解析】

    根据点到x轴上的距离等于其纵坐标的绝对值；点到y轴上的距离等于其横坐标的绝对值即可解答．

    ∵点的坐标为（-4，5），
    ∴点到x轴上的距离等于其纵坐标5的绝对值，即等于5；
    点到y轴上的距离等于其横坐标-4的绝对值，即等于4．
    所以答案分别填5，4．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，将△ABC沿BC方向平移得到△DCE，连接AD，下列条件能够判定四边形ACED为菱形的是（ ）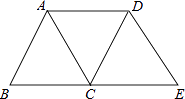

    A.AB=BC
    B.AC=BC
    C.∠B=60°
    D.∠ACB=60°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某农场拟建一间矩形种牛饲养室，饲养室的一面靠现有墙（墙足够长），已知计划中的建筑材料可建围墙的总长度为50m ．设饲养室为长为x（m），占地面积为 ．

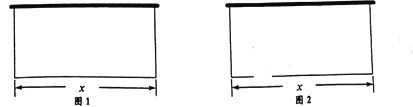
    （1）如图 ，问饲养室为长x为多少时，占地面积y 最大？

    （2）如图，现要求在图中所示位置留2m的门，且仍使饲养室占地面积最大．小敏说：“只要饲养室长比（1）中的长多2m就行了．”请你通过计算，判断小敏的说法是否正确．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AC是矩形ABCD的对角线，过AC的中点O作EF⊥AC，交BC于点E，交AD于点F，连接AE，CF．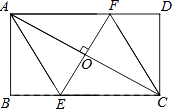

    （1）求证：四边形AECF是菱形；
    （2）若AB= ，∠DCF=30°，求四边形AECF的面积．（结果保留根号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，已知直线AB：y= x+4交x轴于点A，交y轴于点B．直线CD：y=﹣ x﹣1与直线AB相交于点M，交x轴于点C，交y轴于点D．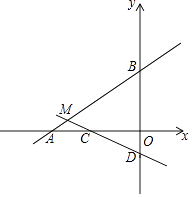

    （1）直接写出点B和点D的坐标；
    （2）若点P是射线MD上的一个动点，设点P的横坐标是x，△PBM的面积是S，求S与x之间的函数关系；
    （3）当S=20时，平面直角坐标系内是否存在点E，使以点B、E、P、M为顶点的四边形是平行四边形？若存在，请直接写出所有符合条件的点E的坐标；若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下表是某校八年级（1）班43名学生右眼视力的检查结果．

    视力

    4.0

    4.1

    4.2

    4.3

    4.4

    4.5

    4.6

    4.7

    4.8

    4.9

    5.0

    人数

    1

    2

    5

    4

    3

    5

    1

    1

    5

    10

    6


    （1）该班学生右眼视力的平均数是（结果保留1位小数）．
    （2）该班学生右眼视力的中位数是 ．
    （3）该班小鸣同学右眼视力是4.5，能不能说小鸣同学的右眼视力处于全班同学的中上水平？试说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】交通工程学理论把在单向道路上行驶的汽车看成连续的流体，并用流量、速度、密度三个概念描述车流的基本特征，其中流量q（辆/小时）指单位时间内通过道路指定断面的车辆数；速度v（千米/小时）指通过道路指定断面的车辆速度，密度k（辆/千米）指通过道路指定断面单位长度内的车辆数．

    为配合大数据治堵行动，测得某路段流量q与速度v之间关系的部分数据如下表：

    （1）根据上表信息，下列三个函数关系式中，刻画q，v关系最准确的是 （只填上正确答案的序号）

    ①q=90v+100；②q=；③．

    （2）请利用（1）中选取的函数关系式分析，当该路段的车流速度为多少时，流量达到最大？最大流量是多少？

    （3）已知q，v，k满足q=vk，请结合（1）中选取的函数关系式继续解决下列问题．

    ①市交通运行监控平台显示，当12≤v＜18时道路出现轻度拥堵．试分析当车流密度k在什么范围时，该路段将出现轻度拥堵；

    ②在理想状态下，假设前后两车车头之间的距离d（米）均相等，求流量q最大时d的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算a·a3的结果是( )

    A. a4B. －a4C. a－3D. －a3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

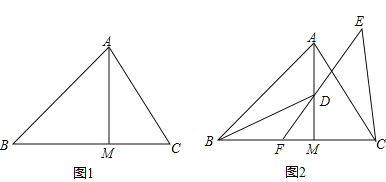
    【题目】在△ABC中，∠ABM=45°，AM⊥BM，垂足为M，点C是BM延长线上一点，连接AC．

    （1）如图1，若AB=3，BC=5，求AC的长；

    （2）如图2，点D是线段AM上一点，MD=MC，点E是△ABC外一点，EC=AC，连接ED并延长交BC于点F，且点F是线段BC的中点，求证：∠BDF=∠CEF．

    查看答案和解析>>

    同步练习册答案