
【题目】一个正三角形和一副三角板(分别含30°和45°)摆放成如图所示的位置,且AB∥CD.则∠1+∠2=__________.
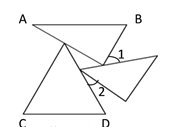
【答案】75°
【解析】
连接AC,根据平行线的性质求出∠BAC+∠ACD=180°,再由∠BAG=30°,∠ECD=60°可得出∠EAC+∠ACE的度数,根据三角形内角和定理得出∠AEC的度数,由补角的定义得出∠GEF的度数,同理可用∠1表示出∠EGF,用∠2表示出∠GFE,再由三角形内角和定理即可得出结论.
解:连接AC,
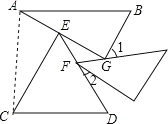
∵AB∥CD,
∴∠BAC+∠ACD=180°,
∵∠BAG=30°,∠ECD=60°,
∴∠EAC+∠ACE=180°-30°-60°=90°,
∵∠CED=60°,
∴∠GEF=180°-90°-60°=30°,
同理∠EGF=180°-∠1-90°=90°-∠1,∠GFE=180°-45°-∠2=135°-∠2,
∵∠GEF+∠EGF+∠GFE=180°,即30°+90°-∠1+135°-∠2=180°,解得∠1+∠2=75°.
故答案为:75°.


科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣x+1与x轴,y轴分别交于B,A两点,动点P在线段AB上移动,以P为顶点作∠OPQ=45°交x轴于点Q.

(1)求点A和点B的坐标;
(2)比较∠AOP与∠BPQ的大小,说明理由.
(3)是否存在点P,使得△OPQ是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线l:y=mx﹣m+1(m为常数,且m≠0)与坐标轴交于A、B两点,若△AOB(O是原点)的面积恰为2,则符合要求的直线l有( )
A.1条
B.2条
C.3条
D.4条
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进甲,乙两种服装后,都加价50%标价出售.春节期间,商场搞优惠促销,决定将甲,乙两种服装分别按标价的七折和八折出售.某顾客购买甲,乙两种服装共付款186元,两种服装标价和为240元.问:这两种服装打折之后售出的利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角梯形ABCD中,![]() ,
,![]() ,
,![]() ,
,![]() .
.
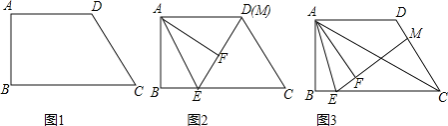
(1)如图1,连接AC,求证:CA是![]() 的平分线;
的平分线;
(2)线段BC上一点E,将![]() 沿AE翻折,点B落到点F处,射线EF与线段CD交于点M.
沿AE翻折,点B落到点F处,射线EF与线段CD交于点M.
①如图2,当点M与点D重合时,求证:![]() ;
;
②如图3,当点M不与点D重合时,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八(1)班同学为了解2018年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,请解答以下问题:


(1)本次调查采用的调查方式是________(填“普查”或“抽样调查”),样本容量是________;
(2)补全频数分布直方图:
(3)若将月均用水量的频数绘成扇形统计图,则月均用水量“![]() ”的圆心角度数是________;
”的圆心角度数是________;
(4)若该小区有5000户家庭,求该小区月均用水量超过![]() 的家庭大约有多少户?
的家庭大约有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题探究】
已知:如图①所示,∠MPN的顶点为P,⊙O的圆心O从顶点P出发,沿着PN方向平移.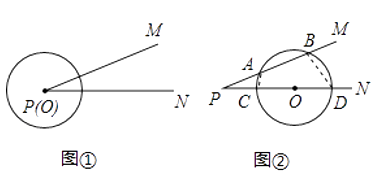
(1)如图②所示,当⊙O分别与射线PM,PN相交于A、B、C、D四个点,连接AC、BD,可以证得△PAC∽△ , 从而可以得到:PAP B=P CP D.
(2)如图③所示,当⊙O与射线PM相切于点A,与射线PN相交于C、D两个点.求证:PA2=PCPD.
(3)【简单应用】
如图④所示,(2)中条件不变,经过点P的另一条射线与⊙O相交于E、F两点.利用上述(1),(2)两问的结论,直接写出线段PA与PE、PF之间的数量关系;当PA=4 ![]() ,EF=2,则PE= .
,EF=2,则PE= . 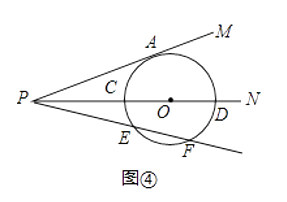
(4)【拓展延伸】如图⑤所示,在以O为圆心的两个同心圆中,A、B是大⊙O上的任意两点,经过A、B 两点作线段,分别交小⊙O于C、E、D、F四个点.求证:ACAE=BDBF.(友情提醒:可直接运用本题上面所得到的相关结论)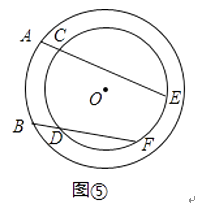
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com