
【题目】已知点P(﹣3a﹣4,2+a),解答下列各题:
(1)若点P在x轴上,则点P的坐标为P ;
(2)若Q(5,8),且PQ∥y轴,则点P的坐标为P ;
(3)若点P在第二象限,且它到x轴、y轴的距离相等,求a2018+2018的值.
【答案】(1)P(2,0);(2)P(5,﹣1);(3)2019
【解析】
(1)若点P在x轴上,点P(x,y)在x轴上![]() y=0,x为任意实数,即2+a=0,a=-2,代入﹣3a﹣4求得P点坐标;
y=0,x为任意实数,即2+a=0,a=-2,代入﹣3a﹣4求得P点坐标;
(2)因为平行于x轴的直线上的点的坐标的特征纵坐标都相等,平行于y轴上的点的坐标的特征横坐标都相等,所以P点横坐标为5,即﹣3a﹣4=5,a=-3代入2+a求得P点坐标;
(3)点P(x,y)到坐标轴及原点的距离:点P(x,y)到x轴的距离等于|y|;点P(x,y)到y轴的距离等于|x|;点P(x,y)到原点的距离等于![]()
解:(1)由题意可得:2+a=0,解得:a=-2,
-3a-4=6-4=2,
所以点P的坐标为(2,0);
(2)根据题意可得:-3a-4=5,解得:a=-3,
2+a=-1,
所以点P的坐标为(5,-1);
(3)根据题意可得:﹣3a﹣4=﹣2﹣a,
解得:a=﹣1,
把a=-1代入a2018+2018=2019.
故答案为:(2,0), (5,-1), 2019.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图1是一台放置在水平桌面上的笔记本电脑,将其侧面抽象成如图2所示的几何图形,若显示屏所在面的侧边AO与键盘所在面的侧边BO长均为24cm,点P为眼睛所在位置,D为AO的中点,连接PD,当PD⊥AO时,称点P为“最佳视角点”,作PC⊥BC,垂足C在OB的延长线上,且BC=12cm. 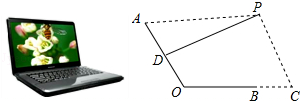
(1)当PA=45cm时,求PC的长;
(2)若∠AOC=120°时,“最佳视角点”P在直线PC上的位置会发生什么变化?此时PC的长是多少?请通过计算说明.(结果精确到0.1cm,可用科学计算器,参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD相交于点O,OE⊥AB于O,若∠BOD=40°,则不正确的结论是( )

A.∠AOC=40° B.∠COE=130° C.∠EOD=40° D.∠BOE=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中有三个点A(1,﹣1)、B(﹣1,﹣1)、C(0,1),点P(0,2)关于A的对称点为P1,P1关于B的对称点为P2,P2关于C的对称点为P3,按此规律继续以A、B、C为对称中心重复前面的操作,依次得到P4、P5、P6,…,则点P2018的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,然后解答后面的问题.
我们知道方程2x+3y=12有无数组解,但在实际生活中我们往往只需要求出其正整数解.例:由2x+3y=12,得![]() ,(x、y为正整数)∴
,(x、y为正整数)∴![]() 则有0<x<6.又
则有0<x<6.又![]() 为正整数,则
为正整数,则![]() 为正整数.
为正整数.
由2与3互质,可知:x为3的倍数,从而x=3,代入![]() =2.
=2.
∴2x+3y=12的正整数解为![]()
问题:
(1)请你写出方程2x+y=5的一组正整数解:_____;
(2)若![]() 为自然数,则满足条件的整数x值有_____个;
为自然数,则满足条件的整数x值有_____个;
A、2 B、3 C、4 D、5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题:①对顶角相等;②同位角相等,两直线平行;③若|a|=|b|,则a=b;④若x=2,则2|x|-1=3.以上命题是真命题的有( ).
A. ①②③④ B. ①④ C. ②④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平行四边形ABCD中,点O是边AD的中点,连接CO并延长交BA延长线于点E,连接ED、AC.
(1)如图1,求证:四边形AEDC是平行四边形;
(2)如图2,若四边形AEDC是矩形,请探究∠COD与∠B的数量关系,写出你的探究结论,并加以证明.
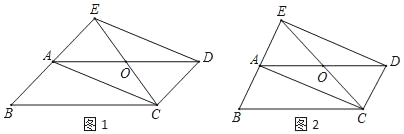
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD∥EF,BC∥AD,AC平分∠BAD且与EF交于点O,那么图中与∠AOE相等的角有( )

A. 3个 B. 4个 C. 5个 D. 6个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com