解:(1)易知:C(0,-4),即OC=4;
故OB=OC=4,B(4,0);
将A(-1,0),B(4,0)代入抛物线的解析式中,得:
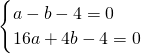
,
解得

;
故抛物线的解析式为:y=x
2-3x-4.
(2)设E(x,0)(0<x<4),易知直线BC:y=x-4,则P(x,x-4),F(x,x
2-3x-4);
故PE=4-x,PF=(x-4)-(x
2-3x-4)=-x
2+4x;
①若S
△PBE:S
△PBF=2:3,
则PE:PF=2:3,
即:
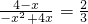
,
解得

,x=4(舍去),
②若S
△PBE:S
△PBF=3:2,则PE:PF=3:2,
即:
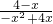
=

,
解得
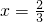
;x=4(舍去)
综上所述,E点的坐标为:E(

,0)或(

,0).
(3)若OE=t,则(t,0);
由(2)知:PE=4-t,则有:
S
△CPE=
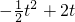
(0≤t≤4);
当t=2时,S取得最大值,最大值为2.
(4)设线段CE的中点为M,即M(1,-2);
若△QCE是以EC为底边的等腰三角形,那么点Q必为线段CE的垂直平分线与抛物线的交点;
由于E(2,0)、C(0,4),
易知直线EC:y=2x-4;
所以设:直线QM:y=-

x+h,
代入M点坐标得:-

+h=-2,
即h=-

;
故直线QM:y=-

x-

,联立抛物线的解析式可得:
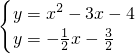
,
解得
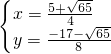
,
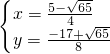
;
故Q
1(
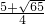
,
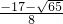
),Q
2(
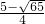
,
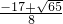
).
分析:(1)根据抛物线的解析式,易得C点的坐标,而OB=OC,即可得到点B的坐标,然后将A、B的坐标代入抛物线的解析式中,通过联立方程组即可求得该抛物线的解析式.
(2)易求得直线BC的解析式,设出点E的横坐标,根据抛物线和直线BC的解析式,即可表示出点P、F的纵坐标,从而得到PE、FP的长,由于△PBE、△PBF等高,那么它们的面积比等于底边的比,然后分:①PE:PF=2:3,②PE:PF=3:2,两种情况进行讨论即可.
(3)若OE=t,则E(t,0),同(2)可求得PE的长,以PE为底、OE长为高即可得到△CPE的面积,从而得到关于△CPE的面积和t的函数关系式,根据所得函数的性质即可求得△CPE的面积最大值及对应的t的值.
(4)设CE的中点为M,若△QEC以EC为底,那么Q必为线段EC的垂直平分线QM与抛物线的交点,由于直线QM与直线CE互相垂直,它们斜率的乘积为-1,结合点M的坐标,即可得到直线QM的长,联立抛物线的解析式,可求得Q点的坐标.
点评:此题主要考查了二次函数解析式的确定、图形面积的求法、二次函数的应用、等腰三角形的判定和性质、函数图象交点坐标的求法等重要知识点,难度适中.

 x轴于E,交抛物线于F.
x轴于E,交抛物线于F.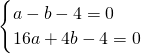 ,
, ;
;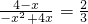 ,
, ,x=4(舍去),
,x=4(舍去),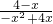 =
= ,
,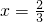 ;x=4(舍去)
;x=4(舍去) ,0)或(
,0)或( ,0).
,0).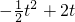 (0≤t≤4);
(0≤t≤4); x+h,
x+h, +h=-2,
+h=-2, ;
; x-
x- ,联立抛物线的解析式可得:
,联立抛物线的解析式可得: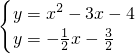 ,
,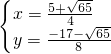 ,
,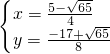 ;
;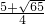 ,
,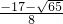 ),Q2(
),Q2(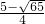 ,
,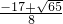 ).
).

 阅读快车系列答案
阅读快车系列答案 与x轴的另一个交点为E.
与x轴的另一个交点为E. 如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=
如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=