
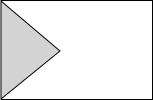
 如图,在周长为12cm的矩形铁板上剪去一个等腰直角三角形(这个等腰直角三角形的底是矩形的宽),则矩形的宽为$\frac{12}{5}$cm时,剩下铁板的面积最大.
如图,在周长为12cm的矩形铁板上剪去一个等腰直角三角形(这个等腰直角三角形的底是矩形的宽),则矩形的宽为$\frac{12}{5}$cm时,剩下铁板的面积最大. 分析 设矩形的宽为xcm,则矩形的长为(6-x)cm,等腰直角三角形的直角边长为($\frac{\sqrt{2}}{2}$x)cm,用矩形面积减去等腰直角三角形的面积得出剩余部分面积的函数解析式,配方成顶点式可得答案.
解答 解:设矩形的宽为xcm,则矩形的长为(6-x)cm,
∴等腰直角三角形的直角边长为$\frac{\sqrt{2}}{2}$x(cm),
则剩下铁板的面积y=x(6-x)-$\frac{1}{2}$•($\frac{\sqrt{2}}{2}$x)•($\frac{\sqrt{2}}{2}$x)
=-$\frac{5}{4}$x2+6x
=-$\frac{5}{4}$(x-$\frac{12}{5}$)2+$\frac{36}{5}$,
∴当x=$\frac{12}{5}$时,y取得最大值$\frac{36}{5}$,
即矩形的宽为$\frac{12}{5}$cm时,剩下铁板的面积最大,
故答案为:$\frac{12}{5}$.
点评 本题主要考查二次函数的应用,掌握矩形和等腰直角三角形的性质得出剩余部分面积的函数解析式是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
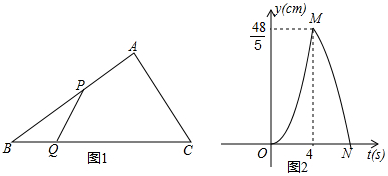
| A. | ①②④ | B. | ②③④ | C. | ①③④ | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 物品重量(千克) | 收取费用(元) |
| 18 | 39 |
| 25 | 60 |
| A. | 120 | B. | 132 | C. | 135 | D. | 150 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
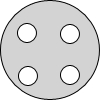 如图,在半径为R的圆形钢板上冲去半径r的四个小圆孔,若R=8.6cm,r=0.7cm,请你利用因式分解的方法计算出剩余钢板的面积.(π取3.14)
如图,在半径为R的圆形钢板上冲去半径r的四个小圆孔,若R=8.6cm,r=0.7cm,请你利用因式分解的方法计算出剩余钢板的面积.(π取3.14)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com