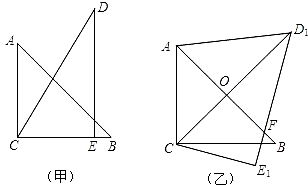
把一副三角板如图甲放置.其中∠ACB=∠DEC=90°.∠A=45°.∠D=30°.斜边AB=12.CD=14.把三角板DCE绕着点C顺时针旋转15°得到△D1CE1.此时AB与CD1交于点O.则线段AD1的长度为1010．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

把一副三角板如图甲放置，其中∠ACB=∠DEC=90°，∠A=45°，∠D=30°，斜边AB=12，CD=14，把三角板DCE绕着点C顺时针旋转15°得到△D₁CE₁（如图乙），此时AB与CD₁交于点O，则线段AD₁的长度为

．

分析：首先由旋转的角度为15°，可知∠ACD₁=45°．已知∠CAO=45°，即可得AO⊥CD₁，然后可在Rt△AOC和Rt△AOD₁中，通过解直角三角形求得AD₁的长．

解答：

解：由题意易知：∠CAB=45°，∠ACD=30°．
若旋转角度为15°，则∠ACO=30°+15°=45°．
∴∠AOC=180°-∠ACO-∠CAO=90°．
在等腰Rt△ABC中，AB=12，则AC=BC=6

．
同理可求得：AO=OC=6．
在Rt△AOD₁中，OA=6，OD₁=CD₁-OC=8，
由勾股定理得：AD₁=10．
故答案为：10．

点评：此题主要考查了旋转的性质以及解直角三角形的综合应用，能够发现AO⊥OC是解决此题的关键．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

把一副三角板如图甲放置，其中∠ACB=∠DEC=90°，∠A=45°，∠D=30°，斜边AB=6cm，DC=7cm把三角板DCE绕点C顺时针旋转15°得到△D₁CE₁（如图乙）．这时AB与CD₁相交于点O，与D₁E₁相交于点F．
（1）求∠OFE₁的度数；
（2）求线段AD₁的长；
（3）若把三角形D₁CE₁绕着点C顺时针再旋转30°得△D₂CE₂，这