
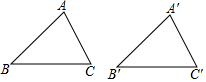
 ①已知AB=A′B′,BC=B′C′,那只要再知道∠B=∠B′,就可以根据“SAS”得到△ABC≌△A′B′C′.
①已知AB=A′B′,BC=B′C′,那只要再知道∠B=∠B′,就可以根据“SAS”得到△ABC≌△A′B′C′.分析 ①要利用SAS,需要两边及其夹角相等,故需要再知道AB和BC的夹角与A′B′和B′C′的夹角相等;
②已知一组边、一组角对应相等,要想利用ASA,则需要再添加一组角,使得这组角和已知那组角的夹边是AB和A′B′即可;
③已知一组角相等,要想利用ASA,则需要再加一组角和这两组角的夹边对应相等即可,可求得答案.
解答 解:
①∵AB=A′B′,BC=B′C′,
∴要使用SAS,则需要添加∠B=∠B′,
故答案为:∠B;∠B′;
②∵AB=A′B′,∠BAC=∠B′A′C′,
∴要使用SAS,则需要添加∠B=∠B′,
故答案为:∠B;∠B′;
③∵∠C=∠C′,
∴要使用SAS,则需要添加∠A=∠A′和AC=A′C′,
故答案为:∠A;∠A′;AC;A′C′.
点评 本题主要考查全等三角形的判定,掌握全等三角形的判定方法是解题的关键,即SSS、SAS、ASA、AAS和HL.


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,一个数阵,每行和每列元素个数都是无限的,但是我们可以按照以下规律,将每个元素都标序(以下右边是数阵中的元素,左边是其序号):1←→a${\;}_{1}^{1}$,2←→a${\;}_{2}^{1}$,3←→a${\;}_{1}^{2}$,4←→a${\;}_{3}^{1}$,5←→a${\;}_{2}^{2}$,6←→a${\;}_{1}^{3}$,7←→a${\;}_{4}^{1}$,…,11←→a${\;}_{5}^{1}$,…,按此规律填写下列空格:18←→${a}_{3}^{3}$,80←→a${\;}_{12}^{2}$.
如图,一个数阵,每行和每列元素个数都是无限的,但是我们可以按照以下规律,将每个元素都标序(以下右边是数阵中的元素,左边是其序号):1←→a${\;}_{1}^{1}$,2←→a${\;}_{2}^{1}$,3←→a${\;}_{1}^{2}$,4←→a${\;}_{3}^{1}$,5←→a${\;}_{2}^{2}$,6←→a${\;}_{1}^{3}$,7←→a${\;}_{4}^{1}$,…,11←→a${\;}_{5}^{1}$,…,按此规律填写下列空格:18←→${a}_{3}^{3}$,80←→a${\;}_{12}^{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,P为AB上的一点,在下列条件中:
如图,在△ABC中,P为AB上的一点,在下列条件中:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com