
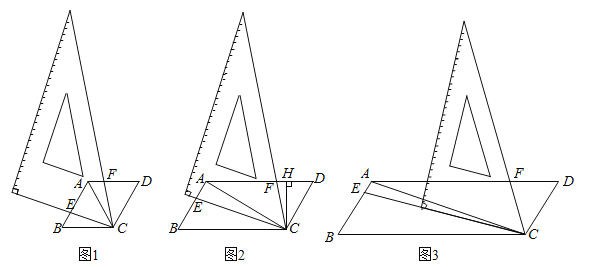
【题目】数学活动课上,某学习小组对有一内角为120°的平行四边形ABCD(∠BAD=120°)进行探究:将一块含60°的直角三角板如图放置在平行四边形ABCD所在平面内旋转,且60°角的顶点始终与点C重合,较短的直角边和斜边所在的两直线分别交线段AB,AD于点E,F(不包括线段的端点).
(1)初步尝试
如图1,若AD=AB,求证:①△BCE≌△ACF,②AE+AF=AC;
(2)类比发现
如图2,若AD=2AB,过点C作CH⊥AD于点H,求证:AE=2FH;
(3)深入探究
如图3,若AD=3AB,探究得:![]() 的值为常数t,则t= .
的值为常数t,则t= .
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
试题分析:(1)①先证明△ABC,△ACD都是等边三角形,再证明∠BCE=∠ACF即可解决问题.②根据①的结论得到BE=AF,由此即可证明.
(2)设DH=x,由由题意,CD=2x,CH=![]() x,由△ACE∽△HCF,得
x,由△ACE∽△HCF,得![]() 由此即可证明.
由此即可证明.
(3)如图3中,作CN⊥AD于N,CM⊥BA于M,CM与AD交于点H.先证明△CFN∽△CEM,得![]() ,由ABCM=ADCN,AD=3AB,推出CM=3CN,所以
,由ABCM=ADCN,AD=3AB,推出CM=3CN,所以![]() =
=![]() ,设CN=a,FN=b,则CM=3a,EM=3b,想办法求出AC,AE+3AF即可解决问题.
,设CN=a,FN=b,则CM=3a,EM=3b,想办法求出AC,AE+3AF即可解决问题.
试题解析:解;(1)①∵四边形ABCD是平行四边形,∠BAD=120°,∴∠D=∠B=60°,∵AD=AB,∴△ABC,△ACD都是等边三角形,∴∠B=∠CAD=60°,∠ACB=60°,BC=AC,∵∠ECF=60°,∴∠BCE+∠ACE=∠ACF+∠ACE=60°,∴∠BCE=∠ACF,在△BCE和△ACF中,∵∠B=∠CAF,BC=AC,∠BCE=∠ACF,∴△BCE≌△ACF;
②∵△BCE≌△ACF,∴BE=AF,∴AE+AF=AE+BE=AB=AC;
(2)设DH=x,由由题意,CD=2x,CH=![]() x,∴AD=2AB=4x,∴AH=AD﹣DH=3x,∵CH⊥AD,∴AC=
x,∴AD=2AB=4x,∴AH=AD﹣DH=3x,∵CH⊥AD,∴AC=![]() =
=![]() x,∴
x,∴![]() ,∴∠ACD=90°,∴∠BAC=∠ACD=90°,∴∠CAD=30°,∴∠ACH=60°,∵∠ECF=60°,∴∠HCF=∠ACE,∴△ACE∽△HCF,∴
,∴∠ACD=90°,∴∠BAC=∠ACD=90°,∴∠CAD=30°,∴∠ACH=60°,∵∠ECF=60°,∴∠HCF=∠ACE,∴△ACE∽△HCF,∴![]() =2,∴AE=2FH.
=2,∴AE=2FH.
(3)如图3中,作CN⊥AD于N,CM⊥BA于M,CM与AD交于点H.
∵∠ECF+∠EAF=180°,∴∠AEC+∠AFC=180°,∵∠AFC+∠CFN=180°,∴∠CFN=∠AEC,∵∠M=∠CNF=90°,∴△CFN∽△CEM,∴![]() ,∵ABCM=ADCN,AD=3AB,∴CM=3CN,∴
,∵ABCM=ADCN,AD=3AB,∴CM=3CN,∴![]() =
=![]() ,设CN=a,FN=b,则CM=3a,EM=3b,∵∠MAH=60°,∠M=90°,∴∠AHM=∠CHN=30°,∴HC=2a,HM=a,HN=
,设CN=a,FN=b,则CM=3a,EM=3b,∵∠MAH=60°,∠M=90°,∴∠AHM=∠CHN=30°,∴HC=2a,HM=a,HN=![]() a,∴AM=
a,∴AM=![]() a,AH=
a,AH=![]() a,∴AC=
a,∴AC=![]() =
=![]() a,AE+3AF=(EM﹣AM)+3(AH+HN﹣FN)=EM﹣AM+3AH+3HN﹣3FN=3AH+3HN﹣AM=
a,AE+3AF=(EM﹣AM)+3(AH+HN﹣FN)=EM﹣AM+3AH+3HN﹣3FN=3AH+3HN﹣AM=![]() a,∴
a,∴![]() =
= =
=![]() .故答案为:
.故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如果两个一次函数y=k1x+b1和y=k2x+b2满足k1=k2,b1≠b2,那么称这两个一次函数为“平行一次函数”.如图,已知函数y=﹣2x+4的图象与x轴、y轴分别交于A、B两点,一次函数y=kx+b与y=﹣2x+4是“平行一次函数”.
(1)若函数y=kx+b的图象过点(3,1),求b的值;
(2)若函数y=kx+b的图象与两坐标轴围成的三角形和△AOB构成位似图形,位似中心为原点,位似比为1:2,求函数y=kx+b的表达式.
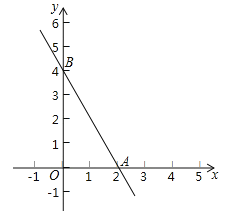
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,我们在2016年7月的日历中标出一个十字星,并计算它的“十字差”(将十字星左右两数,上下两数分别相乘再将所得的积作差,称为该十字星的“十字差”).该十字星的十字差为12×14﹣6×20=48,再选择其它位置的十字星,可以发现“十字差”仍为48. 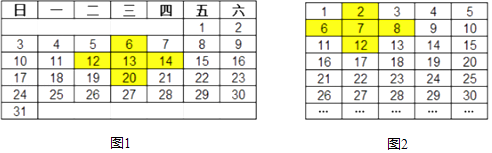
(1)如图2,将正整数依次填入5列的长方形数表中,探究不同位置十字星的“十字差”,可以发现相应的“十字差”也是一个定值,则这个定值为 .
(2)若将正整数依次填入6列的长方形数表中,不同位置十字星的“十字差”是一个定值吗?如果是,请求出这个定值;如果不是,请说明理由.
(3)若将正整数依次填入k列的长方形数表中(k≥3),继续前面的探究,可以发现相应“十字差”为与列数k有关的定值,请用k表示出这个定值,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB=90°,∠COD=30°.
(1)如图1,当点O、A、C在同一条直线上时,∠BOD的度数是;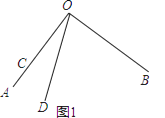
(2)将∠COD从图1的位置开始,绕点O逆时针方向旋转n°(即∠AOC=n°),且0<n<180.
①如果∠COD的一边与∠AOB的一边垂直,则n= .
②当60<n<90时(如图2),作射线OM平分∠AOC,射线ON平分∠BOD,试求∠MON的度数 . 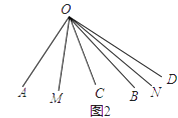
查看答案和解析>>
科目:初中数学 来源: 题型:
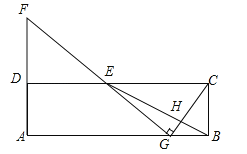
【题目】在矩形ABCD中,E为CD的中点,H为BE上的一点,![]() =3,连接CH并延长交AB于点G,连接GE并延长交AD的延长线于点F.
=3,连接CH并延长交AB于点G,连接GE并延长交AD的延长线于点F.
(1)求证:![]() ;
;
(2)若∠CGF=90°,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com