
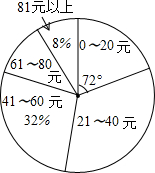
 某校初三(1)班的同学踊跃为“希望工程”捐款,根据捐款情况(捐款数为正数)制作以下统计图表,但班长不小心把墨水滴在统计表上,部分数据看不清楚.根据图表中现有信息解决下列问题:
某校初三(1)班的同学踊跃为“希望工程”捐款,根据捐款情况(捐款数为正数)制作以下统计图表,但班长不小心把墨水滴在统计表上,部分数据看不清楚.根据图表中现有信息解决下列问题:| 捐款 | 人数 |
| 0~20元 | |
| 21~40元 | |
| 41~60元 | |
| 61~80元 | 6 |
| 81元以上 | 4 |
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:解答题
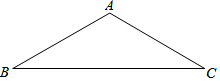 如图,在△ABC中,AB=AC,∠B=30°,BC=12.
如图,在△ABC中,AB=AC,∠B=30°,BC=12.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.25×10-5米 | B. | 25×10-7米 | C. | 2.5×10-6米 | D. | 2.5×10-8米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,AB是⊙O的直径,弦CD⊥AB于点E,⊙O的半径为$\sqrt{3}$,弦CD的长为3cm,则图中阴影部分面积是π-$\frac{3\sqrt{3}}{4}$..
如图,AB是⊙O的直径,弦CD⊥AB于点E,⊙O的半径为$\sqrt{3}$,弦CD的长为3cm,则图中阴影部分面积是π-$\frac{3\sqrt{3}}{4}$..查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com