
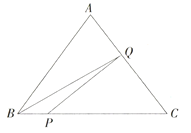
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点P从点B出发,沿BC以每秒2个单位长度的速度向终点C运动,同时点Q从点C出发,沿折线
,点P从点B出发,沿BC以每秒2个单位长度的速度向终点C运动,同时点Q从点C出发,沿折线![]() 以每秒5个单位长度的速度运动,到达点A时,点Q停止1秒,然后继续运动.分别连结PQ、BQ.设
以每秒5个单位长度的速度运动,到达点A时,点Q停止1秒,然后继续运动.分别连结PQ、BQ.设![]() 的面积为S,点P的运动时间为
的面积为S,点P的运动时间为![]() 秒.
秒.
(1)求点A与BC之间的距离.
(2)当![]() 时,求
时,求![]() 的值.
的值.
(3)求S与![]() 之间的函数关系式.
之间的函数关系式.
(4)当线段PQ与![]() 的某条边垂直时,直接写出
的某条边垂直时,直接写出![]() 的值.
的值.
【答案】(1)4;(2)![]() 或
或![]() ;(3)当0<t≤1时,
;(3)当0<t≤1时,![]() ;当1<t≤2时,
;当1<t≤2时,![]() ;当2<t≤3时,
;当2<t≤3时,![]() ;(4)
;(4)![]() 或
或![]() 或
或![]() .
.
【解析】
(1)作AD⊥BC于点D,利用等腰三角形的三线合一可得BD=3,再利用勾股定理即可求得AD的长;
(2)分两种情况讨论,当0<t≤1时,点Q在AC上;当2<t≤3时,点Q在AB上,先用含t 的代数式表示BP和AQ的长,再根据![]() 列出方程求解即可;
列出方程求解即可;
(3)分三种情况讨论,当0<t≤1时,点Q在AC上,当1<t≤2时,点Q与点A重合;当2<t≤3时,点Q在AB上,画出相应的图形,过点Q作QE⊥BC于点E,根据相似三角形的性质可表示出QE的长,进而可得S与t的函数关系式;
(4)分三种情况讨论,当PQ⊥AC时,当PQ⊥BC时,当PQ⊥AB时,画出相应的图形,利用相似三角形的性质列出方程求解即可.
(1)如图,作AD⊥BC于点D.
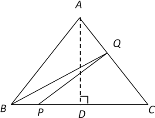
∵AB=AC=5,AD⊥BC,BC=6,
∴BD=![]() BC=3.
BC=3.
∴在Rt△ABD中,AD=![]() .
.
(2)当0<t≤1时,由题意可知:BP=2t,AQ=5-5t,
∵![]() ,
,
∴![]() ,
,
解得![]() .
.
当2<t≤3时,由题意可知:BP=2t,AQ=5(t-2)=5t-10,
∵![]() ,
,
∴![]() ,
,
解得![]() .
.
综上所述,当![]() 时,
时,![]() 的值为
的值为![]() 或
或![]() .
.
(3)当0<t≤1时,如图,点Q在AC上,过点Q作QE⊥BC于点E,
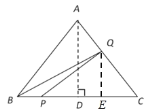
∵AD⊥BC,QE⊥BC,
∴AD∥QE,
∴△QEC∽△ADC,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
当1<t≤2时,如图,点Q与点A重合,
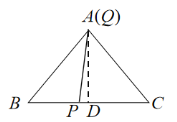
则![]() ,
,
∴![]() ;
;
当2<t≤3时,如图,点Q在AB上,过点Q作QE⊥BC于点E,
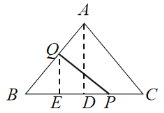
∵AD⊥BC,QE⊥BC,
∴AD∥QE,
∴△QEB∽△ADB,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
综上所述:当0<t≤1时,![]() ;当1<t≤2时,
;当1<t≤2时,![]() ;当2<t≤3时,
;当2<t≤3时,![]() ;
;
(4)当PQ⊥AC时,如图,
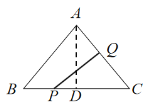
∵AD⊥BC,PQ⊥AC,
∴∠ADC=∠PQC=90°,
又∵∠C=∠C,
∴△PQC∽△ADC,
∴![]() ,
,
∴![]() ,
,
解得:![]() ,
,
当PQ⊥BC时,
由题意可知此时点Q与点A重合,且点P与点D重合,如图,
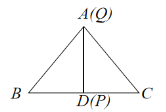
则BP=BD=3,
∴2t=3,
解得:![]() ,
,
当PQ⊥AB时,如图,
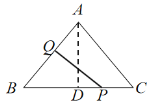
∵AD⊥BC,PQ⊥AB,
∴∠ADB=∠PQB=90°,
又∵∠B=∠B,
∴△PQB∽△ADB,
∴![]() ,
,
∴![]() ,
,
解得:![]() ,
,
综上所述:当线段PQ与![]() 的某条边垂直时,t的值为
的某条边垂直时,t的值为![]() 或
或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】求二次函数![]() 的图象如图所示,其对称轴为直线
的图象如图所示,其对称轴为直线![]() ,与
,与![]() 轴的交点为
轴的交点为![]() 、
、![]() ,其中
,其中![]() ,有下列结论:①
,有下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() ;其中,正确的结论有( )
;其中,正确的结论有( )
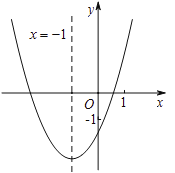
A.5B.4C.3D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年,随着电子产品的广泛应用,学生的近视发生率出现低龄化趋势,引起了相关部门的重视.某区为了了解在校学生的近视低龄化情况,对本区7-18岁在校近视学生进行了简单的随机抽样调查,并绘制了以下两幅不完整的统计图.

请根据图中信息,回答下列问题:
(1)这次抽样调查中共调查了近视学生 人;
(2)请补全条形统计图;
(3)扇形统计图中10-12岁部分的圆心角的度数是 ;
(4)据统计,该区7-18岁在校学生近视人数约为10万,请估计其中7-12岁的近视学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,C为⊙O上一点,BG与⊙O相切于点B,交AC的延长线于点D(点D在线段BG上),AC = 8,tan∠BDC =![]()
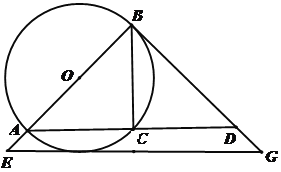
(1)求⊙O的直径;
(2)当DG=![]() 时,过G作
时,过G作![]() ,交BA的延长线于点E,说明EG与⊙O相切.
,交BA的延长线于点E,说明EG与⊙O相切.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,AB是直径,AP是过点A的切线,点C在
中,AB是直径,AP是过点A的切线,点C在![]() 上,点D在AP上,且
上,点D在AP上,且![]() ,延长DC交AB于点E.
,延长DC交AB于点E.
(1)求证:![]() .
.
(2)若![]() 的半径为5,
的半径为5,![]() ,求
,求![]() 的长.(结果保留
的长.(结果保留![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
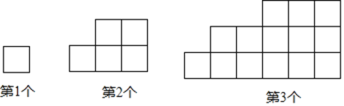
【题目】下列图形都是由大小相同的小正方形按一定规律组成的,其中第1个图形的周长为4,第2个图形的周长为10,第3个图形的周长为18,…,按此规律排列,回答下列问题:
(1)第5个图形的周长为 ;
(2)第![]() 个图形的周长为 ;
个图形的周长为 ;
(3)若第![]() 个图形的周长为180,则
个图形的周长为180,则![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
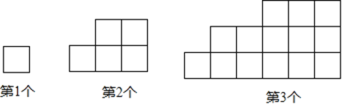
【题目】下列图形都是由大小相同的小正方形按一定规律组成的,其中第1个图形的周长为4,第2个图形的周长为10,第3个图形的周长为18,…,按此规律排列,回答下列问题:
(1)第5个图形的周长为 ;
(2)第![]() 个图形的周长为 ;
个图形的周长为 ;
(3)若第![]() 个图形的周长为180,则
个图形的周长为180,则![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
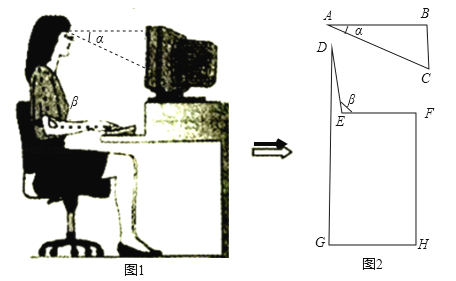
【题目】(2017江西省)如图1,研究发现,科学使用电脑时,望向荧光屏幕画面的“视线角”α约为20°,而当手指接触键盘时,肘部形成的“手肘角”β约为100°.图2是其侧面简化示意图,其中视线AB水平,且与屏幕BC垂直.
(1)若屏幕上下宽BC=20cm,科学使用电脑时,求眼睛与屏幕的最短距离AB的长;
(2)若肩膀到水平地面的距离DG=100cm,上臂DE=30cm,下臂EF水平放置在键盘上,其到地面的距离FH=72cm.请判断此时β是否符合科学要求的100°?
(参考数据:sin69°≈![]() ,cos21°≈
,cos21°≈![]() ,tan20°≈
,tan20°≈![]() ,tan43°≈
,tan43°≈![]() ,所有结果精确到个位)
,所有结果精确到个位)
查看答案和解析>>
科目:初中数学 来源: 题型:
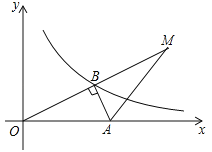
【题目】如图,在平面直角坐标系中,Rt△AOB的斜边OA在x轴的正半轴上,∠OBA=90°,且tan∠AOB=![]() ,OB=
,OB=![]() ,反比例函数
,反比例函数![]() 的图象经过点B.
的图象经过点B.
(1)求反比例函数的表达式;
(2)若△AMB与△AOB关于直线AB对称,一次函数y=mx+n的图象过点M、A,求一次函数的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com