
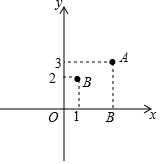
 在平面直角坐标系中,点A的坐标为(3,3),点B的坐标为(1,2).
在平面直角坐标系中,点A的坐标为(3,3),点B的坐标为(1,2).分析 (1)利用两点间距离公式计算即可.
(2)根据点A与点A′关于原点对称,即可解决问题.
(3)因为⊙A与⊙A′关于原点对称,直线m也是关于原点对称,所以当直线m与⊙A相交时,S3=S1,因为S2+S3=π•($\sqrt{5}$)2=5π,即可推出S1+S2=S3+S2=5π.
解答 解:(1)∵A(3,3),B(1,2),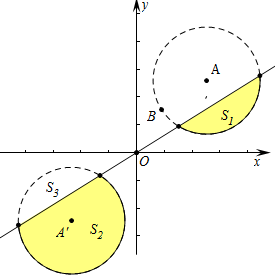
∴AB=$\sqrt{(3-1)^{2}+(3-2)^{2}}$=$\sqrt{5}$,
以A为圆心,线段AB的长度为半径作⊙A如图所示,
故答案为$\sqrt{5}$
(2)⊙A关于点O的对称图形⊙A′如图所示,A′(-3,-3).
故答案为(-3,-3).
(3)∵⊙A与⊙A′关于原点对称,直线m也是关于原点对称,
∴当直线m与⊙A相交时,S3=S1,
∵S2+S3=π•($\sqrt{5}$)2=5π,
∴S1+S2=S3+S2=5π.
故答案为5π.
点评 本题考查圆综合题、两点间距离公式、中心对称的性质、圆面积公式等知识,解题的关键是学会利用割补法求面积,属于中考常考题型.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2x2 | B. | 2y2 | C. | y2-x2 | D. | x2-y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,把一张矩形的纸片沿图中的虚线裁成三张大小相同的小矩形纸片.若得到的小矩形纸片与原来大矩形纸片相似,则大矩形纸片的长与宽的比值为$\sqrt{3}$.
如图,把一张矩形的纸片沿图中的虚线裁成三张大小相同的小矩形纸片.若得到的小矩形纸片与原来大矩形纸片相似,则大矩形纸片的长与宽的比值为$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若ab=ac,则b=c | B. | 若a=b,则$\frac{a}{{c}^{2}+1}$=$\frac{b}{{c}^{2}+1}$ | ||
| C. | 若$\frac{b}{a}$=$\frac{c}{a}$两边都除以a,可得b=c | D. | 若S=ab,则b=$\frac{s}{a}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -6、1 | B. | 6、1 | C. | 6、-1 | D. | -6、-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x=70%×84 | B. | x=(1+70%)×84 | C. | 84=70%x | D. | 84=(1-70%)x |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com