
分析 根据三角形重心性质可得:3GI2=AI2+BI2+CI2-(AG2+BG2+CG2),求得GI后代入求值即可.
解答 解:三角形重心性质:3GI2=AI2+BI2+CI2-(AG2+BG2+CG2),
∵AB=c=6,CA=b=5,BC=a=4.
∴2s=a+b+c=15.
又∵AI2=$\frac{bc(s-a)}{s}$.AG2=$\frac{2{b}^{2}+2{c}^{2}-{a}^{2}}{9}$,
∴AI2+BI2+CI2=[(a+b+c)(bc+ca+ab)-6abc]÷(a+b+c)=26,
AG2+BG2+CG2=(a2+b2+c2)÷3=$\frac{77}{3}$,
∴3GI2=26-$\frac{77}{3}$=$\frac{1}{3}$,
∴GI=$\frac{1}{3}$,
∴GI:BC=$\frac{1}{3}$:5=$\frac{1}{15}$.
点评 本题考查了三角形的五心的知识,解题的关键是了解三角形重心性质:3GI2=AI2+BI2+CI2-(AG2+BG2+CG2).


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
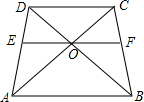 在梯形ABCD中,CD∥AB,AC、BD交于点O,过点O作AB的平行线交AD于点E,交BC于点F,则图中有5对相似形三角形;若DC=9,AB=15,则OD:OB=$\frac{3}{5}$,EF=$\frac{45}{4}$.
在梯形ABCD中,CD∥AB,AC、BD交于点O,过点O作AB的平行线交AD于点E,交BC于点F,则图中有5对相似形三角形;若DC=9,AB=15,则OD:OB=$\frac{3}{5}$,EF=$\frac{45}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com