
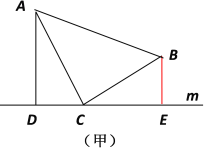
【题目】如图:△ABC中CA=CB, ∠ACB=90°,直线m经过点C,AD⊥m,BE⊥m,垂足分别是点D、E.
(1)在图(甲)中,求证:△ACD≌△CBE.你能探索出线段AD、BE、DE之间的关系吗?
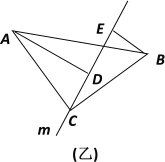
(2)在图(乙)中上面的结论还成立吗?为什么?
【答案】(1)证明见解析,DE=AD+BE;(2)成立,理由见解析
【解析】试题分析:(1)根据垂直的性质,可根据“AAS”证明△ADC ≌△CEB,然后根据全等三角形的性质证明即可;
(2)同(1)的证明方法直接可证明.
试题解析:DE=AD+BE
(1)证明:∵AD⊥m ∴∠DAC﹢∠ACD=∠ADC=90°
∵∠ACB=90°∴∠ACD+∠BCE=90°
∴∠DAC=∠BCE
∵BE⊥m ∴∠BEC=90°
在△ADC 和△CEB中
∠ADC=∠CEB=90°
∠DAC=∠BCE
CA=CB
∴△ADC ≌△CEB (AAS)
∴AD=CE DC=BE (全等三角形的对应边相等)
∵DE=DC+CE ∴DE=AD+BE
(2) 在(乙)图中上面的结论仍然成立.
证明:∵AD⊥m ∴∠ADC=90°∠ACD+∠CAD=90°
∵BE⊥m ∴∠CEB=90°
∵∠ACB=90°∴∠ACD+∠BCE=90°
∴∠DAC=∠ECB
在△ADC 和△CEB中
∠ADC=∠CEB=90°
∠DAC=∠ECB
CA=CB
∴△ADC ≌△CEB (AAS)
∴AD=CE DC=BE (全等三角形的对应边相等)
∵DE=DC+CE ∴DE=AD+BE


科目:初中数学 来源: 题型:
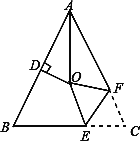
【题目】如图,在△ABC中,AB=AC,∠BAC=64°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC为_________度.
查看答案和解析>>
科目:初中数学 来源: 题型:
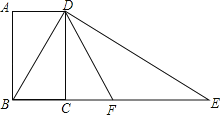
【题目】如图,四边形ABCD为矩形,过点D作对角线BD的垂线,交BC的延长线于点E,取BE的中点F,连接DF,DF=4.设AB=x,AD=y,则x2+(y﹣4)2的值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com