
【题目】如图信息,L1为走私船,L2为我公安快艇,航行时路程与时间的函数图象,问 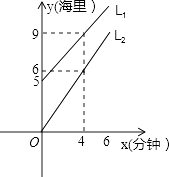
(1)在刚出发时我公安快艇距走私船多少海里?
(2)计算走私船与公安快艇的速度分别是多少?
(3)写出L1 , L2的解析式
(4)问6分钟时两艇相距几海里.
(5)猜想,公安快艇能否追上走私船,若能追上,那么在几分钟追上?
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
【题目】下列各多项式中,能用公式法分解因式的是( )
A. a2-b2+2ab B. a2+b2+ab C. 25n2+15n+9 D. 4a2+12a+9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在△ABC中,∠ACB=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥MN于M,BN⊥MN于N. 
(1)求证:MN=AM+BN.
(2)若过点C在△ABC内作直线MN,AM⊥MN于M,BN⊥MN于N,则AM、BN与MN之间有什么关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的解答过程,求y2+4y+8的最小值.
解:y2+4y+8=y2+4y+4+4=(y+2)2+4≥4,∵(y+2)2≥0即(y+2)2的最小值为0,
∴y2+4y+8的最小值为4.
仿照上面的解答过程,求m2+m+4的最小值和4﹣x2+2x的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学生在一学年的6次测验中,语文、数学成绩分别为(单位:分):
语文:80,84,88,76,79,85
数学:80,75,90,64,88,95
试估计该学生是数学成绩稳定还是语文成绩稳定?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com