
 已知AB∥DE,BF、DF分别平分∠ABC,∠CDE,求∠C、∠F的关系.
已知AB∥DE,BF、DF分别平分∠ABC,∠CDE,求∠C、∠F的关系. 分析 根据平行线的性质可得∠ABC+∠CDC+∠C=360°,由此得出∠FBC+∠CDF的值,再根据四边形的内角和为360°可得出∠C、∠F的关系.
解答 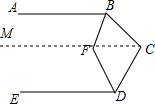 解:过C作CM∥AB,
解:过C作CM∥AB,
则AB∥DE∥CM,
∴∠ABC+∠BCM=∠EDC+∠DCM=180°,
∴∠ABC+∠CDE+∠C=360°,
∴∠C=360°-(∠ABC+∠CDE),
∵BF、DF分别平分∠ABC,∠CDE,
∴∠FBC+∠CDF=$\frac{1}{2}$(∠ABC+∠CDE),
又∵四边形的内角和为360°,
∴∠F+∠C=360-$\frac{1}{2}$(∠ABC+∠CDE),
∴$∠F=180°-\frac{1}{2}∠C$.
点评 本题考查平行线的性质和四边形的内角和,关键在于掌握两直线平行同位角相等,内错角相等,同旁内角互补的性质.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com