
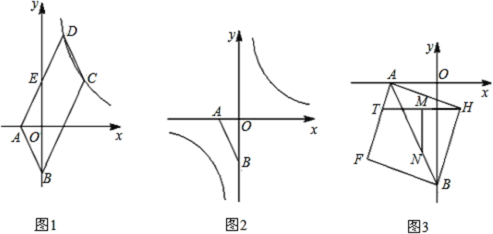
【题目】如图1,已知点![]() ,
,![]() ,且
,且![]() 、
、![]() 满足
满足![]() ,
,![]() 的边
的边![]() 与
与![]() 轴交于点
轴交于点![]() ,且
,且![]() 为
为![]() 中点,双曲线
中点,双曲线![]() 经过
经过![]() 、
、![]() 两点.
两点.
(1)求![]() 的值;
的值;
(2)点![]() 在双曲线
在双曲线![]() 上,点
上,点![]() 在
在![]() 轴上,若以点
轴上,若以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,试求满足要求的所有点
为顶点的四边形是平行四边形,试求满足要求的所有点![]() 、
、![]() 的坐标;
的坐标;
(3)以线段![]() 为对角线作正方形
为对角线作正方形![]() (如图
(如图![]() ,点
,点![]() 是边
是边![]() 上一动点,
上一动点,![]() 是
是![]() 的中点,
的中点,![]() ,交
,交![]() 于
于![]() ,当
,当![]() 在
在![]() 上运动时,
上运动时,![]() 的值是否发生改变?若改变,求出其变化范围;若不改变,请求出其值,并给出你的证明.
的值是否发生改变?若改变,求出其变化范围;若不改变,请求出其值,并给出你的证明.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ;
;![]() ,
,![]() ;
;![]() ,
,![]() ;(3)
;(3)![]() 的值不发生改变
的值不发生改变![]() .
.
【解析】
(1)先根据非负数的性质求出![]() 、
、![]() 的值,故可得出
的值,故可得出![]() 、
、![]() 两点的坐标,设
两点的坐标,设![]() ,由
,由![]() ,可知
,可知![]() ,再根据反比例函数的性质求出
,再根据反比例函数的性质求出![]() 的值即可;
的值即可;
(2)由(1)知![]() 可知反比例函数的解析式为
可知反比例函数的解析式为![]() ,再由点
,再由点![]() 在双曲线
在双曲线![]() 上,点
上,点![]() 在
在![]() 轴上,设
轴上,设![]() ,
,![]() ,再分以
,再分以![]() 为边和以
为边和以![]() 为对角线两种情况求出
为对角线两种情况求出![]() 的值,故可得出
的值,故可得出![]() 、
、![]() 的坐标;
的坐标;
(3)连![]() 、
、![]() 、
、![]() ,易证
,易证![]() ,故
,故![]() ,
,![]() ,
,![]() 由此即可得出结论.
由此即可得出结论.
(1)![]()
![]() ,
,
![]()
![]() ,
,
解得:![]() ,
,
![]() ,
,![]() ,
,
![]() 为
为![]() 中点,
中点,
![]() ,
,
设![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(2)![]() 由(1)知
由(1)知![]() ,
,
![]() 反比例函数的解析式为
反比例函数的解析式为![]() ,
,
![]() 点
点![]() 在双曲线
在双曲线![]() 上,点
上,点![]() 在
在![]() 轴上,
轴上,
![]() 设
设![]() ,
,![]() ,
,
①当![]() 为边时:
为边时:
如图1,若![]() 为平行四边形,
为平行四边形,
则![]() ,
,
解得![]() ,
,
此时![]() ,
,![]() ;
;
如图2,若![]() 为平行四边形,
为平行四边形,
则![]() ,
,
解得![]() ,
,
此时![]() ,
,![]() ;
;
②如图3,当![]() 为对角线时,
为对角线时,
![]() ,且
,且![]() ;
;
![]()
![]() ,
,
解得![]() ,
,
![]() ,
,![]() ;
;
故![]() ,
,![]() ;
;![]() ,
,![]() ;
;![]() ,
,![]() ;
;
(3)![]() 的值不发生改变,
的值不发生改变,
理由:如图4,连![]() 、
、![]() 、
、![]() ,
,
![]() 是线段
是线段![]() 的垂直平分线,
的垂直平分线,
![]() ,
,
![]() 四边形
四边形![]() 是正方形,
是正方形,
![]() ,
,
在![]() 与
与![]() 中,
中,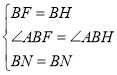 ,
,
![]() ,
,
![]() ,
,
![]() ,
,
四边形![]() 中,
中,![]() ,而
,而![]() ,
,
所以,![]() ,所以,四边形
,所以,四边形![]() 内角和为
内角和为![]() ,
,
所以![]() .
.
![]() ,
,
![]()
![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,分别以△ABC的边AC和BC为腰向外作等腰直角△DAC和等腰直角△EBC,连接DE.
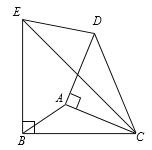
(1)求证:△DAC∽△EBC;
(2)求△ABC与△DEC的面积比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a≠0)与x轴的一个交点坐标为(2,0),对称轴是直线x=1,其图象的一部分如图所示,对于下列说法:其中正确的是( )
①抛物线过原点:
②a﹣b+c<0:
③2a+b+c=0;
④抛物线顶点为(1,![]() ):
):
⑤当x<1时,y随x的增大而增大
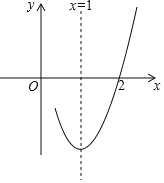
A.①②③B.①③④C.①④⑤D.③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
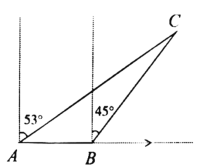
【题目】如图,渔船跟踪鱼群由西向东航行,到达A处时,测得小岛C位于它的北偏东53°方向,再航行![]() 后达到B处(
后达到B处(![]() ),测得小岛C位于它的北偏东45°方向.小岛C的周围
),测得小岛C位于它的北偏东45°方向.小岛C的周围![]() 内有暗礁,如果渔船不改变航向继续向东航行,请你通过计算说明渔船有无触礁的危险?
内有暗礁,如果渔船不改变航向继续向东航行,请你通过计算说明渔船有无触礁的危险?
(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】深圳国际马拉松赛事设有A“全程马拉松”,B“半程马拉松”,C“嘉年华马拉松”三个项目,小智和小慧参加了该赛事的志愿者服务工作,组委会将志愿者随机分配到三个项目组.
(1)小智被分配到A“全程马拉松”项目组的概率为 .
(2)用树状图或列表法求小智和小慧被分到同一个项目标组进行志愿服务的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 过点
过点![]() 和点
和点![]() ,连结AB交y轴于点C.
,连结AB交y轴于点C.
(1)求抛物线的函数解析式;
(2)点P在线段AB下方的抛物线上运动,连结AP,BP. 设点P的横坐标为m,△ABP的面积为s.
①求s与m的函数关系式;
②当s取最大值时,抛物线上是否存在点Q,使得S△ACQ=s. 若存在,求点Q的坐标;若不存在,说明理由.
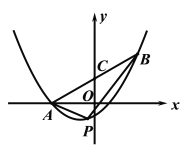
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,点O在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线与AC的延长线相交于点P.
(1)求证:PD是⊙O的切线;
(2)求证:△ABD∽△DCP;
(3)当AB=5cm,AC=12cm时,求线段PC的长.
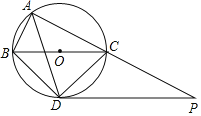
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边△ABC和点P,设点P到△ABC三边AB、AC、BC的距离分别为h1,h2,h3,△ABC的高为h.
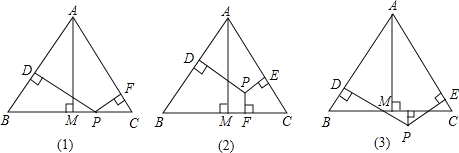
(1)若点P在一边BC上,如图①,此时h3=0,求证:h1+h2+h3=h;
(2)当点P在△ABC内,如图②,以及点P在△ABC外,如图③,这两种情况时,上述结论是否成立?若成立,请予以证明;若不成立,h1,h2,h3与h之间又有怎样的关系,请说出你的猜想,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
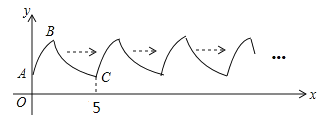
【题目】如图,曲线AB是抛物线![]() 的一部分(其中A是抛物线与y轴的交点,B是顶点),曲线BC是双曲线
的一部分(其中A是抛物线与y轴的交点,B是顶点),曲线BC是双曲线![]() 的一部分.曲线AB与BC组成图形W由点C开始不断重复图形W形成一组“波浪线”.若点
的一部分.曲线AB与BC组成图形W由点C开始不断重复图形W形成一组“波浪线”.若点![]() ,
,![]() 在该“波浪线”上,则m的值为________,n的最大值为________.
在该“波浪线”上,则m的值为________,n的最大值为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com