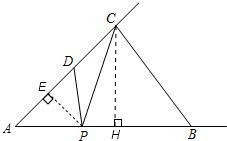
解:(1)作CH⊥AB,垂足为点H,设CH=m;
∵
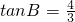
,∴
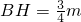
∵∠A=45°,∴AH=CH=m
∴
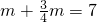
;
∴m=4;
∴△ABC的面积等于
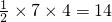
;
(2)∵AH=CH=4,
∴
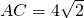
∵∠DPA=∠ACB,∠A=∠A,
∴△ADP∽△ABC;
∴
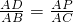
,即
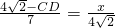
∴
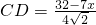
;
作PE⊥AC,垂足为点E;
∵∠A=45°,AP=x,
∴
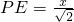
;
∴所求的函数解析式为
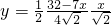
,即
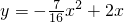
;
当D到C时,AP最大.
∵△CPA∽△BCA
∴
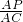
=

∴AP=
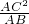
=
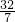
,
∴定义域为0<x<
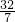
;
(3)由△ADP∽△ABC,得
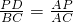
,即
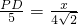
;
∴
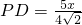
;
∵△PCD是以PD为腰的等腰三角形,
∴有PD=CD或PD=PC;
(i)当点D在边AC上时,
∵∠PDC是钝角,只有PD=CD
∴
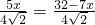
;
解得
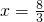
;
(ii)当点D在边AC的延长线上时,
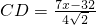
,
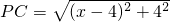
如果PD=CD,那么
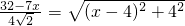
解得x=16
如果PD=PC,那么
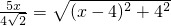
解得x
1=32,
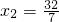
(不符合题意,舍去)
综上所述,AP的长为

,或16,或32.
分析:(1)过C作CH⊥AB于H,在Rt△ACH、Rt△CHB中,分别用CH表示出AH、BH的长,进而由AB=AH+BH=7求出CH的长,即可得到AH、BH的长,由三角形的面积公式可求得△ABC的面积;
(2)由∠DPA=∠ACB,可证得△DPA∽△BCA,根据相似三角形得出的成比例线段可求得AD的表达式,进而可得到CD的长;过P作PE⊥AC于E,根据AP的长及∠A的度数即可求得PE的长;以CD为底、PE为高即可求得△PCD的面积,由此可得出y、x的函数关系;
求自变量取值的时,关键是确定AP的最大值,由于P、D分别在线段AB、AC上,AP最大时D、C重合,可根据相似三角形得到的比例线段求出此时AP的长,由此可得到x的取值范围;
(3)在(2)题中,已证得△ADP∽△ABC,根据相似三角形得到的比例线段,可得到PD的表达式;若△PDC是以PD为腰的等腰三角形,则可分两种情况:PD=DC或PD=PC;
①如果D在线段AC上,此时∠PDC是钝角,只有PD=DC这一种情况,联立两条线段的表达式,即可求得此时x的值;
②如果D在线段AC的延长线上,可根据上面提到的两种情况,分别列出关于x的等量关系式,即可求得x的值.
点评:此题考查了解直角三角形、相似三角形的判定和性质、等腰三角形的判定和性质、二次函数的应用等知识,同时还考查了分类讨论的数学思想方法,难度较大.

 已知在△ABC中,∠A=45°,AB=7,
已知在△ABC中,∠A=45°,AB=7,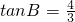 ,动点P、D分别在射线AB、AC上,且∠DPA=∠ACB,设AP=x,△PCD的面积为y.
,动点P、D分别在射线AB、AC上,且∠DPA=∠ACB,设AP=x,△PCD的面积为y. 解:(1)作CH⊥AB,垂足为点H,设CH=m;
解:(1)作CH⊥AB,垂足为点H,设CH=m;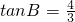 ,∴
,∴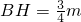
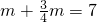 ;
;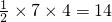 ;
;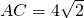
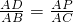 ,即
,即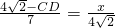
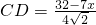 ;
;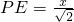 ;
;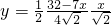 ,即
,即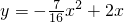 ;
;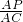 =
=
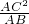 =
=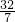 ,
,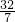 ;
;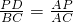 ,即
,即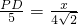 ;
;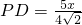 ;
;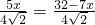 ;
;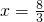 ;
;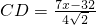 ,
,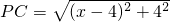
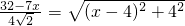
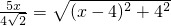
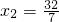 (不符合题意,舍去)
(不符合题意,舍去) ,或16,或32.
,或16,或32.

 如图,已知在△ABC中,∠B与∠C的平分线交于点P.
如图,已知在△ABC中,∠B与∠C的平分线交于点P.