
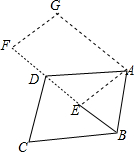
 如图,将平行四边形ABCD绕点A顺时针旋转,其中B、C、D分别落在点E,F、G处,且点B、E、D、F在一直线上,若CD=4,BC=2$\sqrt{7}$,则平行四边形ABCD的面积为8$\sqrt{2}$.
如图,将平行四边形ABCD绕点A顺时针旋转,其中B、C、D分别落在点E,F、G处,且点B、E、D、F在一直线上,若CD=4,BC=2$\sqrt{7}$,则平行四边形ABCD的面积为8$\sqrt{2}$. 分析 先利用旋转的性质得∠1=∠2,AB=AE,再证明∠1=∠3,则可判断△BAE∽△BDA,得到∠AEB=∠DAB,然后证明AD=BD,由勾股定理求得CD边上的高,求得S△BCD,即可求得结论.
解答 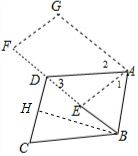 解:∵平行四边形ABCD绕点A旋转到平行四边形AEFG的位置,点E恰好是对角线BD的中点,
解:∵平行四边形ABCD绕点A旋转到平行四边形AEFG的位置,点E恰好是对角线BD的中点,
∴∠1=∠2,AB=AE,
∵EF∥AG,
∴∠2=∠3,
∴∠1=∠3,
∵∠ABE=∠DBA,
∴△BAE∽△BDA,
∴∠AEB=∠DAB,
∵AE=AB,
∴∠AEB=∠ABD,
∴∠ABD=∠DAB,
∴DB=DA=BC=2$\sqrt{7}$,
过B作BH⊥CD于H,
则CH=DH=2,
∴BH=$\sqrt{B{C}^{2}-C{H}^{2}}$=$\sqrt{(2\sqrt{7})^{2}-{2}^{2}}$=2$\sqrt{2}$,
∴S△BCD=$\frac{1}{2}$CD•BH=4$\sqrt{2}$,
∴平行四边形ABCD的面积=2S△BCD=8$\sqrt{2}$,
故答案为:8$\sqrt{2}$.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.解决本题的关键是证明△BAE∽△BDA,


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{5}{3}$ | B. | -$\frac{5}{3}$ | C. | $\frac{3}{5}$ | D. | -$\frac{3}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 全班数学成绩的平均数 | B. | 全班数学成绩的众数 | ||
| C. | 全班数学成绩的中位数 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{x}{300}$=$\frac{2x+1.5}{300}$-93 | B. | $\frac{x}{300}$=$\frac{2x+1.5}{300}$+93 | ||
| C. | $\frac{x}{300}$=$\frac{2x+1.5}{300}$-$\frac{93}{3600}$ | D. | $\frac{x}{300}$=$\frac{2x+1.5}{300}$+$\frac{93}{3600}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
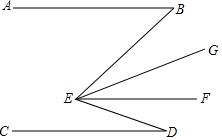 已知:如图,AB∥EF∥CD,EG平分∠BEF,∠B+∠BED+∠D=192°,∠B-∠D=24°,则∠GEF的度数为( )
已知:如图,AB∥EF∥CD,EG平分∠BEF,∠B+∠BED+∠D=192°,∠B-∠D=24°,则∠GEF的度数为( )| A. | 50° | B. | 40° | C. | 30° | D. | 20° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com