
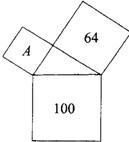
 1、三个正方形的面积如下图,正方形A的面积为( )
1、三个正方形的面积如下图,正方形A的面积为( )科目:初中数学 来源: 题型:


查看答案和解析>>
科目:初中数学 来源: 题型:
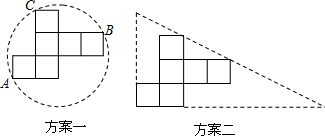
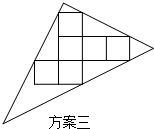
| 纸片被利用的面积 | 纸片的总面积 |
查看答案和解析>>
科目:初中数学 来源: 题型:
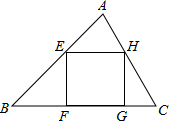 某课题学习小组在一次活动中对三角形的内接正方形的有关问题进行了探讨:
某课题学习小组在一次活动中对三角形的内接正方形的有关问题进行了探讨:查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2011-2012学年广东省沭阳县广宇学校九年级第一次月考考试数学卷 题型:解答题
某数学研究所门前有一个边长为4米的正方形花坛,花坛内部要用红、黄、紫三种颜色的花草种植成如图所示的图案,图案中 .准备在形如Rt
.准备在形如Rt 的四个全等三角形内种植红色花草,在形如Rt△EMH的四个全等三角形内种植黄色花草,在正方形
的四个全等三角形内种植红色花草,在形如Rt△EMH的四个全等三角形内种植黄色花草,在正方形 内种植紫色花草,每种花草的价格如下表:
内种植紫色花草,每种花草的价格如下表:
| 品种 | 红色花草 | 黄色花草 | 紫色花草 |
| 价格(元/米2) | 60 | 80 | 120 |
 的长为
的长为 米,正方形
米,正方形 的面积为
的面积为 平方米,买花草所需的费用为
平方米,买花草所需的费用为 元,解答下列问题:
元,解答下列问题: 与
与 之间的函数关系式为
之间的函数关系式为 ;
; 与
与 之间的函数关系式,并求所需的最低费用是多少元;
之间的函数关系式,并求所需的最低费用是多少元; 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com