
分析 (1)将分式中能分解因式的进行因式分解,再化简求出答案;
(2)将分式中能分解因式的进行因式分解,再化简求出答案.
解答 解:(1)$\frac{{x}^{2}-1}{{x}^{2}-2x+1}$÷$\frac{x+1}{x-1}$•$\frac{1-x}{1+x}$,
=$\frac{(x+1)(x-1)}{(x-1)^{2}}$×$\frac{x-1}{x+1}$•$\frac{1-x}{1+x}$
=$\frac{1-x}{1+x}$,
把x=$\frac{1}{2}$代入上式得:
原式=$\frac{1-\frac{1}{2}}{1+\frac{1}{2}}$=$\frac{1}{3}$;
(2)$\frac{{x}^{2}-4x+4}{{x}^{2}-4}$÷$\frac{x-2}{{x}^{2}+2x}$+3
=$\frac{(x-2)^{2}}{(x-2)(x+2)}$×$\frac{x(x+2)}{x-2}$+3
=x+3,
把x=-3.2代入上式得:原式=-3.2+3=-0.2.
点评 此题主要考查了分式的化简求值,正确分解因式进而化简分式是解题关键.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
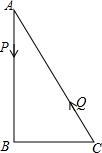 如图所示,在△ABC中,AB=12cm,BC=5cm,AC=13cm,动点P从点A出发沿线段AB向点B运动,速度为2cm/s,动点Q从点C出发沿线段CA向点A运动,B速度为1cm/s.运动时间为多少时AQ=2AP?
如图所示,在△ABC中,AB=12cm,BC=5cm,AC=13cm,动点P从点A出发沿线段AB向点B运动,速度为2cm/s,动点Q从点C出发沿线段CA向点A运动,B速度为1cm/s.运动时间为多少时AQ=2AP?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com