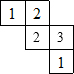
由一些大小相同的小正方体搭成的几何体的俯视图如图所示.其正方形中的数字表示该位置上的小正方体的个数.画出该几何体的主视图．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

2．

由一些大小相同的小正方体搭成的几何体的俯视图如图所示，其正方形中的数字表示该位置上的小正方体的个数，画出该几何体的主视图．

分析由已知条件可知，主视图有3列，每列小正方数形数目分别为1，2，3；据此可画出图形．

解答解：如图所示：

点评本题考查几何体的三视图画法．由几何体的俯视图及小正方形内的数字，可知主视图的列数与俯视数的列数相同，且每列小正方形数目为俯视图中该列小正方形数字中的最大数字．

练习册系列答案

金钥匙期末冲刺100分系列答案

名师指导期末冲刺卷系列答案

初中英语听力训练苏州大学出版社系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：填空题

12．已知a：b：c=2：3：4，且a-2b+3c=20，则a+2b-3c=-10．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

13．

如图，AD是△BAC的平分线，DE⊥AB于E，DF⊥AC于F．
（1）求证：DE=DF；
（2）求证：AD垂直平分EF．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

10．根据下列材料，解答问题：
等比数列求和：
概念：对于一列数a₁，a₂，a₃，…a_n，…（n为正整数），若从第二个数开始，每一个数与前一个数的比为一定值，即$\frac{{a}_{k}}{{a}_{k-1}}$=q（常数），那么这一列数a₁，a₂，a₃，…，a_n，…成等比数列，这一常数q叫做该数列的公比．
例：求等比数列$\frac{1}{3}$，$\frac{1}{{3}^{2}}$，$\frac{1}{{3}^{3}}$，…，$\frac{1}{{3}^{n}}$的和．
解：令S=$\frac{1}{3}$+$\frac{1}{{3}^{2}}$+$\frac{1}{{3}^{3}}$+…+$\frac{1}{{3}^{8}}$①，则3S=1+$\frac{1}{3}$+$\frac{1}{{3}^{2}}$+$\frac{1}{{3}^{3}}$+…+$\frac{1}{{3}^{7}}$②
由②-①得：2S=1-$\frac{1}{{3}^{8}}$=$\frac{{3}^{8}-1}{{3}^{8}}$，即S=$\frac{{3}^{8}-1}{2×{3}^{8}}$．
（1）模仿例题，求等比数列$\frac{1}{4}$，$\frac{1}{{4}^{2}}$，$\frac{1}{{4}^{3}}$，…，$\frac{1}{{4}^{10}}$的和；
（2）填空：数列$\frac{1}{a}$，$\frac{1}{{a}^{2}}$，…$\frac{1}{{a}^{n}}$，（a≠1，n为正整数）的公比q=$\frac{1}{a}$，该数列各项的和为$\frac{{a}^{n}-1}{（a-1）{a}^{n}}$．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

17．已知点A（2a-b，5+a），B（2b-1，-a+b）．
（1）若点A，B关于x轴对称，求a，b的值；
（2）若A，B关于y轴对称，求（4a+b）²⁰¹⁶的值．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

7．计算：
（1）-9+5×（-6）-12÷（-6）；
（2）36×（-$\frac{1}{6}$+$\frac{3}{4}$+$\frac{1}{3}$-$\frac{1}{12}$）；
（3）-1²-（1-0.5）×$\frac{1}{3}$×[2-（-3）²]．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

14．

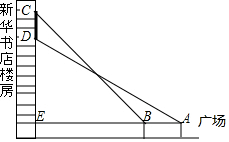如图，小刚同学在广场上观测新华书店楼房墙上的电子屏幕CD，点A是小刚的眼睛，测得屏幕下端D处的仰角为30°，然后他正对屏幕方向前进了6m到达B处，又测得该屏幕上端C处的仰角为45°，延长AB与楼房垂直相交于点E，测得BE=21m，则该屏幕上端与下端之间的距离CD为（21-9$\sqrt{3}$）m．