
分析 (1)设安排甲种货车x辆,则安排乙种货车(9-x)辆,由“甲型货车每辆可装饮用水5吨和粮食1吨,乙型货车每辆可装饮用水3吨和粮食2吨”和“要运送30吨饮用水和13吨粮食”得:$\left\{\begin{array}{l}{5x+3(9-x)≥30}\\{x+2(9-x)≥13}\end{array}\right.$,求解即可;
(2)设租车费用为w元,则由“甲、乙两种货车的租车费用每辆分别为4000元、3500元”得:w=4000x+3500(9-x),利用一次函数的性质求解;
(3)设安排甲种货车x辆,则安排乙种货车y辆费用更低,根据题意得$\left\{\begin{array}{l}{5x+3y=30}\\{x+2y=13}\end{array}\right.$,求解即可.
解答 解:(1)设安排甲种货车x辆,则安排乙种货车(9-x)辆,
由题意得:$\left\{\begin{array}{l}{5x+3(9-x)≥30}\\{x+2(9-x)≥13}\end{array}\right.$,
解得:1.5≤x≤5,
∵x为正整数且x≤4,
∴x=2,3,4,
∴安排甲、乙两种货车方案共有下表3种:
| 方案 | 方案一 | 方案二 | 方案三 |
| 甲种货车 | 2 | 3 | 4 |
| 乙种货车 | 7 | 6 | 5 |
点评 本题考查的是用一次函数解决实际问题,此类题是近年中考中的热点问题.注意利用一次函数求最值时,关键是应用一次函数的性质;即由函数y随x的变化,结合自变量的取值范围确定最值.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,E为△ABC中AB边的中点,D为△ABC外一点,且DE⊥AB,过点D作DN⊥AC于点N,DM⊥BC交BC的延长线于点M,已知AN=BM,求证:点D在△ABC的外角平分线上.
如图,E为△ABC中AB边的中点,D为△ABC外一点,且DE⊥AB,过点D作DN⊥AC于点N,DM⊥BC交BC的延长线于点M,已知AN=BM,求证:点D在△ABC的外角平分线上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
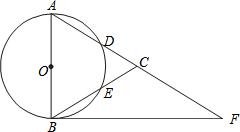 如图,在△ABC中,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且AC=CF,∠CBF=∠CFB.
如图,在△ABC中,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且AC=CF,∠CBF=∠CFB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
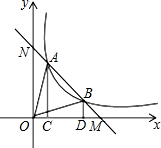 如图,一次函数y=kx+b(k≠0)与反比例函数y=$\frac{2}{x}$交于点A(1,2),与x轴交于点M,与y轴交于点N.
如图,一次函数y=kx+b(k≠0)与反比例函数y=$\frac{2}{x}$交于点A(1,2),与x轴交于点M,与y轴交于点N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
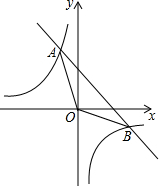 一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于A(-1,$\sqrt{3}$)、B($\sqrt{3}$,n)两点.
一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于A(-1,$\sqrt{3}$)、B($\sqrt{3}$,n)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小军和小虎两人从同一条路同时从学校出发到图书馆查阅资料,学校与图书馆的路程是4千米.小军骑自行车,小虎步行,当小军从原路返回到学校时,小虎刚好到达图书馆.图中折线O-A-B-C和线段OD分别表示两人离学校的路程s(千米)与所经过的时间t(分钟)之间的函数关系,请根据图象回答下列问题:
小军和小虎两人从同一条路同时从学校出发到图书馆查阅资料,学校与图书馆的路程是4千米.小军骑自行车,小虎步行,当小军从原路返回到学校时,小虎刚好到达图书馆.图中折线O-A-B-C和线段OD分别表示两人离学校的路程s(千米)与所经过的时间t(分钟)之间的函数关系,请根据图象回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com