
分析 (1)先把方程变形为x2-6x=-4,再根据配方法得到(x-3)2=5,然后利用直接开平方法求解;
(2)根据配方法得到(x-6)2=35,然后利用直接开平方法求解;
(3)利用因式分解法解方程;
(4)利用因式分解法解方程.
解答 解:(1)x2-6x=-4,
x2-6x+9=-4+9,
(x-3)2=5,
x-3=±$\sqrt{5}$,
所以x1=3+$\sqrt{5}$,x2=3-$\sqrt{5}$;
(2))x2-12x=-1,
x2-12x+36=-1+36,
(x-6)2=35,
x-6=±$\sqrt{35}$,
所以x1=6+$\sqrt{35}$,x2=6-$\sqrt{35}$;
(3)(x+9)(x-1)=0,
x+9=0或x-1=0,
所以x1=-9,x2=1;
(4)(2t+1)(t-4)=0,
2t+1=0或t-4=0,
所以t1=-$\frac{1}{2}$,x2=4.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了配方法解一元二次方程.


科目:初中数学 来源: 题型:解答题
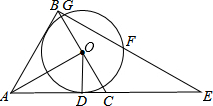 如图,△ABC是等边三角形,AO⊥BC,垂足为点O,⊙O与AC相切于点D,BE⊥AB交AC的延长线于点E,与⊙O相交于G、F两点.
如图,△ABC是等边三角形,AO⊥BC,垂足为点O,⊙O与AC相切于点D,BE⊥AB交AC的延长线于点E,与⊙O相交于G、F两点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①④ | C. | ②④ | D. | ② |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y<0 | B. | y≤0 | C. | y>m | D. | y≥m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
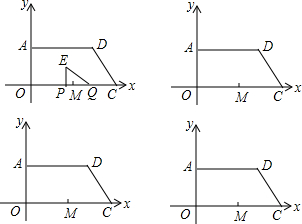
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,将图中的点(-5,2),(-3,4),(-1,2),(-4,2),(-2,2),(-2,3),(-4,3)做如下变化:
如图所示,将图中的点(-5,2),(-3,4),(-1,2),(-4,2),(-2,2),(-2,3),(-4,3)做如下变化:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 把图一的长方形纸片ABCD折叠,B、C两点恰好重合落在AD边上的点P处(如图二),已知∠MPN=90°,PM=3,PN=4,
把图一的长方形纸片ABCD折叠,B、C两点恰好重合落在AD边上的点P处(如图二),已知∠MPN=90°,PM=3,PN=4,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com