
.在△ABC和△ADC中,有下列三个论断:①AB=AD;②∠BAC=∠DAC;③BC=DC.将两个论断作为条件,另一个论断作为结论构成一个正确的因果关系,则条件是__________,结论为__________.
.①AB=AD;②∠BAC=∠DAC,③BC=DC 或①AB=AD;③BC=DC,②∠BAC=∠DAC.
解析考点:全等三角形的判定与性质.
分析:根据全等三角形的判定方法SAS,可知当①②为条件且AC为公共边时结论③成立;根据全等三角形的判定方法SSS,可知当①③为条件且AC为公共边时结论②立;
解:方案一∵AB=AD,∠BAC=∠DAC,AC为公共边,
∴△ABC≌△ADC,
∴BC=DC;
方案二:∵AB=AD,BC=DC,AC为公共边,
∴△ABC≌△ADC,
∴∠BAC=∠DAC.
故答案为:条件:①AB=AD;②∠BAC=∠DAC或①AB=AD;③BC=DC;结论为:③BC=DC或∠BAC=∠DAC.


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 22、完成下列证明:
22、完成下列证明:
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
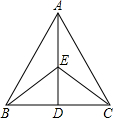 如图:已知AD是△ABC中BC边上的高,E是AD上一点,EB=EC,∠ABE=∠ACE.求证:∠BAE=∠CAE.
如图:已知AD是△ABC中BC边上的高,E是AD上一点,EB=EC,∠ABE=∠ACE.求证:∠BAE=∠CAE.
|
查看答案和解析>>
科目:初中数学 来源: 题型:
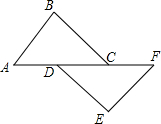 如图,在△ABC和△FED中,AD=FC,AB=FE,当添加条件
如图,在△ABC和△FED中,AD=FC,AB=FE,当添加条件查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com