
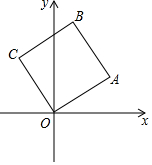
 已知直角坐标系中边长为1的正方形OABC,A、B,两点在第一象限.OA与x轴的角为30°,那么点B的坐标是($\frac{\sqrt{3}-1}{2}$,$\frac{\sqrt{3}+1}{2}$).
已知直角坐标系中边长为1的正方形OABC,A、B,两点在第一象限.OA与x轴的角为30°,那么点B的坐标是($\frac{\sqrt{3}-1}{2}$,$\frac{\sqrt{3}+1}{2}$). 分析 作AD⊥x轴于D,BE⊥x轴于E,AF⊥BE于F,如图,只要证明△AFB≌△ADO,求出OE、BE即可解决问题.
解答 解:作AD⊥x轴于D,BE⊥x轴于E,AF⊥BE于F,如图,
四边形OABC为正方形,∴AB=AO,
∵AF⊥FB,
∴∠AFB=90°,
∵AD⊥OD,
∴∠ADO=90°,
∵∠BAO=∠FAD=90°,
∴∠BAF=∠OAD,
在△AFB和△ADO中,
$\left\{\begin{array}{l}{∠BAF=∠OAD}\\{∠AFB=∠ADO}\\{AB=AO}\end{array}\right.$
∴△AFB≌△ADO.
∴BF=OD,AF=AD,
∴点B的横坐标为DO-DE=DO-AF=DO-AD=1•cos30°-1•sin30°=$\frac{\sqrt{3}-1}{2}$;
点B的纵坐标为EF+FB=AD+DO=1•sin30°+1•cos30°=$\frac{\sqrt{3}+1}{2}$,
故答案为($\frac{\sqrt{3}-1}{2}$,$\frac{\sqrt{3}+1}{2}$).
点评 本题考查正方形的性质、全等三角形的判定和性质.直角三角形39度角寻找等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
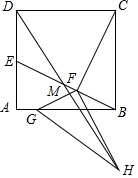 如图,正方形ABCD的边长为4,点E是AD的中点,连接BE,过点C作CF⊥BE交BE于点F,将△FBC绕F顺时针旋转得△FGH,使得点G落到线段AB上,连接DH交BE于点M,则DM的长度是$\frac{4}{11}$$\sqrt{89}$.
如图,正方形ABCD的边长为4,点E是AD的中点,连接BE,过点C作CF⊥BE交BE于点F,将△FBC绕F顺时针旋转得△FGH,使得点G落到线段AB上,连接DH交BE于点M,则DM的长度是$\frac{4}{11}$$\sqrt{89}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小彬所在的“数学兴趣小组”对函数y=(x-1)(x-2)(x-3)的图象与性质进行了探究,探究过程如下,请补充完整.
小彬所在的“数学兴趣小组”对函数y=(x-1)(x-2)(x-3)的图象与性质进行了探究,探究过程如下,请补充完整.| x | … | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| y | … | m | -24 | -6 | 0 | 0 | 0 | 6 | 24 | 60 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在正方形ABCD中,AB=4$\sqrt{5}$,E为BC中点,连接AE,点F为AE上一点,FE=2,FG⊥AE交DC于G,将GF绕着G点逆时针旋转使得F点正好在AD上的点H处,过点H作HN⊥HG交AB于N点,交AE于M点,则S△MNF=$\frac{96\sqrt{5}-192}{5}$.
在正方形ABCD中,AB=4$\sqrt{5}$,E为BC中点,连接AE,点F为AE上一点,FE=2,FG⊥AE交DC于G,将GF绕着G点逆时针旋转使得F点正好在AD上的点H处,过点H作HN⊥HG交AB于N点,交AE于M点,则S△MNF=$\frac{96\sqrt{5}-192}{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com