
【题目】如图,在平面直角坐标系中![]() ,点
,点![]() 是
是![]() 轴正半轴上一动点,点
轴正半轴上一动点,点![]() 、
、![]() 在
在![]() 轴正半轴上.
轴正半轴上.
(1)如图1,若![]() ,
,![]() ,
,![]() 、
、![]() 是
是![]() 的两条角平分钱,且
的两条角平分钱,且![]() 、
、![]() 交于点
交于点![]() ,直接写出
,直接写出![]() 的长度 ;
的长度 ;
(2)如图2,![]() 是等边三角形,以线段
是等边三角形,以线段![]() 为边在第一象限内作等边
为边在第一象限内作等边![]() ,连接
,连接![]() 并延长,交
并延长,交![]() 轴于点
轴于点![]() ,当点
,当点![]() 运动到什么位置时,满足
运动到什么位置时,满足![]() ?求点
?求点![]() 的坐标;
的坐标;
(3)如图3,以![]() 为边在
为边在![]() 的下方作等边
的下方作等边![]() ,点
,点![]() 在
在![]() 轴上运动时,求
轴上运动时,求![]() 的最小值.
的最小值.



【答案】(1)4;(2)C(8,0);(3)1
【解析】
(1)作![]() ,CH 交BD的延长线于H,分别证明
,CH 交BD的延长线于H,分别证明![]() 和
和![]() ,根据全等三角形对应边相等即可得出答案;
,根据全等三角形对应边相等即可得出答案;
(2)证明![]() ,根据全等三角形的性质得到
,根据全等三角形的性质得到![]() ,求出CD,得出答案;
,求出CD,得出答案;
(3)以OA为对称轴作等边![]() ,连接EP,并延长EP交x轴于点F,证明点P在直线EF上运动,根据垂线段最短解答.
,连接EP,并延长EP交x轴于点F,证明点P在直线EF上运动,根据垂线段最短解答.
解:(1)作![]() ,CH 交BD的延长线于H,
,CH 交BD的延长线于H,

∵![]()
∴![]()
∴![]()
∵![]() ,
,![]()
∴![]()
∵![]() 是
是![]() 的角平分钱
的角平分钱
∴![]()
∴![]() ,
,![]()
∴![]()
在![]() 和
和![]() 中,
中,
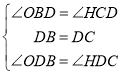
∴![]()
∴![]()
在![]() 和
和![]() 中,
中,
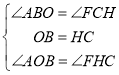
∴![]()
![]()
∴![]()
故答案为:4;
(2)∵![]() 、
、![]() 是等边三角形,
是等边三角形,
∴![]()
∴![]()
在![]() 和
和![]() 中,
中,

∴![]()
![]()
∴![]()
∴![]()
∴![]()
∴![]() ,即
,即![]()
∴点C的坐标为:![]() ;
;
(3)以OA为对称轴作等边![]() ,连接EP,并延长EP交x轴于点F,
,连接EP,并延长EP交x轴于点F,
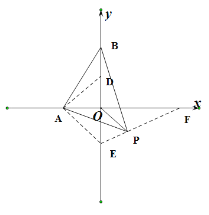
由(2)得,![]()
∴![]()
∴![]()
∴![]()
∴点P在直线EF上运动,当![]() 时,OP最小
时,OP最小
∴![]()
∴OP最小值为1.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC为等边三角形,D为边BA延长线上一点,连接CD,以CD为一边作等边三角形CDE,连接AE.
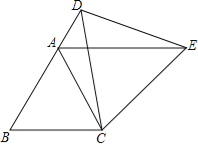
(1)求证:△CBD≌△CAE.
(2)判断AE与BC的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一种新运算“♀”,观察下列运算:
(+5)♀(+14)=+19,
![]() ♀
♀![]() =+20,
=+20,
![]() ,
,
![]() ,
,
![]() ,
,
(+13)♀0=+13.
(1)请你认真思考上述运算,归纳运算“♀”的法则.
两数进行运算“♀”时,同号______,异号_________,特别地,0和任何数进行运算“♀”,或任何数和0进行运算“♀”,结果都为_______.
(2)计算:![]() ♀[0♀
♀[0♀![]() ].
].
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形OABC中,O为平面直角坐标系的原点,点A坐标为(a,0),点C的坐标为(0,b),且a、b满足![]() +|b-6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的线路移动.
+|b-6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的线路移动.
(1)a=______________,b=_____________,点B的坐标为_______________;
(2)当点P移动4秒时,请指出点P的位置,并求出点P的坐标;
(3)在移动过程中,当点P到x轴的距离为5个单位长度时,求点P移动的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言人数的比为5:2,请结合图中相关数据回答下列问题:
(1)则样本容量容量是______________,并补全直方图;
(2)该年级共有学生500人,请估计全年级在这天里发言次数不少于12的次数;
(3)已知A组发言的学生中恰有1位女生,E组发言的学生中有2位男生,现从A组与E组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好是一男一女的概率。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“节能环保”是对美好家园的一种守护,某汽车制造厂生产一种新型能源汽车,计划半年后每月生产汽车20辆,由于另有任务,每月上班人数不一定相等,实际每月生产量与计划量相比情况如下表(增加为正,减少为负):
月份 | 一 | 二 | 三 | 四 | 五 | 六 |
增减(辆) | +3 | -2 | -1 | +4 | +2 | -5 |
(1)生产量最多的一个月,比生产量最少的一个月多生产多少辆?
(2)半年内总生产量是多少?比计划多了还是少了?多或少多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,D是AB的中点,过点B作∠CBE=∠A,BE与射线CA相交于点E,与射线CD相交于点F.
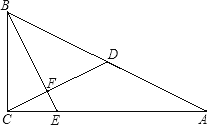
(1)如图,当点E在线段CA上时,求证:BE⊥CD;
(2)若BE=CD,那么线段AC与BC之间具有怎样的数量关系?并证明你所得到的结论;
(3)若△BDF是等腰三角形,求∠A的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AC=BC,∠ACB=120°,点D在AB边上运动(D不与A、B重合),连结CD.作∠CDE=30°,DE交AC于点E.

(1)当DE∥BC时,△ACD的形状按角分类是直角三角形;
(2)在点D的运动过程中,△ECD的形状可以是等腰三角形吗?若可以,请求出∠AED的度数;若不可以,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AE是∠BAC的角平分线,交BC于点E,DE∥AB交AC于点D.
(1)求证AD=ED;
(2)若AC=AB,DE=3,求AC的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com