
���� ��1�����ø��ʹ�ʽֱ�Ӽ��㼴�ɣ�
��2���б��õ����п��ܽ�������ҵ���īˮ�ֱʺ�һ֧��īˮ�ֱʵ�����������������ʣ�
��� �⣺��1������A��B��֧Ϊ����ɫīˮ�ֱʣ�����C��D��֧Ϊ����ɫīˮ�ֱʣ�
��������ľߺ������ȡһ֧�ֱʣ������õ���īˮ�ֱʵĸ���=$\frac{2}{4}$=$\frac{1}{2}$��
��2���б����������£�
| A | B | C | D | |
| A | ��A��B�� | ��A��C�� | ��A��D�� | |
| B | ��B��A�� | ��B��C�� | ��B��D�� | |
| C | ��C��A�� | ��C��B�� | ��C��D�� | |
| D | ��D��A�� | ��D��B�� | ��D��C�� |
���� ���⿼��������б�������״ͼ������ʣ��б������Բ��ظ�����©���г����п��ܵĽ�����ʺ���������ɵ��¼�����״ͼ���ʺ�����������������ɵ��¼�������ʱҪע������ǷŻ�ʵ�黹�Dz��Ż�ʵ�飮�õ���֪ʶ��Ϊ������=������������������֮�ȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -��+5����+��-5�� | B�� | -��-5����+��-5�� | C�� | -��-5����+��+5�� | D�� | +��-5����-5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
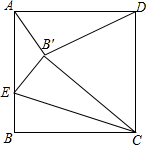 ��ͼ��������ABCD�У�AB=2����E��AB��һ�㣬����������CE�۵�����B������������һ��B'��������AB'DΪ���������Σ���BE�ij���Ϊ4-2$\sqrt{3}$��$\frac{2\sqrt{3}}{3}$��
��ͼ��������ABCD�У�AB=2����E��AB��һ�㣬����������CE�۵�����B������������һ��B'��������AB'DΪ���������Σ���BE�ij���Ϊ4-2$\sqrt{3}$��$\frac{2\sqrt{3}}{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1��2��3��4 | B�� | $\sqrt{2}$��$\sqrt{3}$��1��$\sqrt{6}$ | C�� | 2��4��6��8 | D�� | 2��5��3��10 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
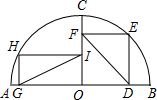 ��ͼ��C���Ե�OΪԲ�ģ�ABΪֱ���İ�Բ��һ�㣬��CO��AB����OC����ֱ�������OGHI��������ODEF���ҵ�I��F��OC�ϣ���H��E�ڰ�Բ�ϣ���֤��IG=FD��С�Ʒ�������ͼ����֪��õ������߶Σ����֤��IG=FD��
��ͼ��C���Ե�OΪԲ�ģ�ABΪֱ���İ�Բ��һ�㣬��CO��AB����OC����ֱ�������OGHI��������ODEF���ҵ�I��F��OC�ϣ���H��E�ڰ�Բ�ϣ���֤��IG=FD��С�Ʒ�������ͼ����֪��õ������߶Σ����֤��IG=FD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
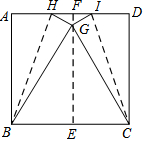 ��ͼ����������ABCD���ۣ�ʹ��A����D�غϣ���B��C�غϣ��ۺ�EF��չ�����ٴ��۵���ʹ��A���D�غ����������ڵ�G�����ۺ۷ֱ�ΪBH��CI�����������ABCD�ı߳���2�������н��ۣ��١�GBC�ǵȱ������Σ��ڡ�IGH�������7$\sqrt{3}$-12����tan��BHA=2+$\sqrt{3}$����GE=2$\sqrt{3}$��������ȷ�ĸ����У�������
��ͼ����������ABCD���ۣ�ʹ��A����D�غϣ���B��C�غϣ��ۺ�EF��չ�����ٴ��۵���ʹ��A���D�غ����������ڵ�G�����ۺ۷ֱ�ΪBH��CI�����������ABCD�ı߳���2�������н��ۣ��١�GBC�ǵȱ������Σ��ڡ�IGH�������7$\sqrt{3}$-12����tan��BHA=2+$\sqrt{3}$����GE=2$\sqrt{3}$��������ȷ�ĸ����У�������| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com