
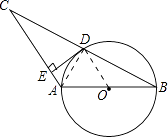
【题目】如图,⊙O的直径AB=4,∠ABC=30°,BC交⊙O于D,D是BC的中点. 
(1)求BC的长;
(2)过点D作DE⊥AC,垂足为E,求证:直线DE是⊙O的切线.
【答案】
(1)解:连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°,
又∵∠ABC=30°,AB=4,
∴BD=2 ![]() ,
,
∵D是BC的中点,
∴BC=2BD=4 ![]()
(2)证明:连接OD.
∵D是BC的中点,O是AB的中点,
∴DO是△ABC的中位线,
∴OD∥AC,则∠EDO=∠CED
又∵DE⊥AC,
∴∠CED=90°,∠EDO=∠CED=90°
∴DE是⊙O的切线.
【解析】(1)根据圆周角定理求得∠ADB=90°,然后解直角三角形即可求得BD,进而求得BC即可;(2)要证明直线DE是⊙O的切线只要证明∠EDO=90°即可.
【考点精析】通过灵活运用含30度角的直角三角形和圆周角定理,掌握在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半即可以解答此题.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】在军事上,常用时钟表示方向角(读数对应的时针方向),如正北为12点方向,北偏西30°为11点方向.在一次反恐演习中,甲队员在A处掩护,乙队员从A处沿12点方向以40米/分的速度前进,2分钟后到达B处.这时,甲队员发现在自己的1点方向的C处有恐怖分子,乙队员发现C处位于自己的2点方向(如图).假设距恐怖分子100米以外为安全位置.
(1)乙队员是否处于安全位置?为什么?
(2)因情况不明,甲队员立即发出指令,要求乙队员沿原路后撤,务必于15秒内到达安全位置.为此,乙队员至少应用多快的速度撤离?(结果精确到个位.参考数据:![]() ,
,![]() .)
.)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在学习《圆》这一章时,老师给同学们布置了一道尺规作图题:
尺规作图:过圆外一点作图的切线。
已知:P为圆O外一点。
求作:经过点P的圆O的切线。
小敏的作法如下:
①连接OP,作线段OP的垂直平分线MN交OP于点C;
②以点C为圆心,CO的长为半径作圆交圆O于A、B两点;
③作直线PA、PB,所以直线PA、PB就是所求作的切线。
老师认为小敏的作法正确.
请回答:连接OA,OB后,可证∠OAP=∠OBP=90°,其依据是;由此可证明直线PA,PB都是⊙O的切线,其依据是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF、BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC.
(1)求证:OE=OF;
(2)求∠ACB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于P.若四边形ABCD的面积是18,则DP的长是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:(1)20+(﹣14)﹣(﹣18)﹣13; (2)﹣2![]() ;
;
(3)(﹣7)×(﹣5)﹣90÷(﹣15) (4)-120×![]() +(-7)×
+(-7)×![]() +37×
+37×![]()
(5)﹣14﹣(1﹣0.5)×![]() ×[2-(-3)2].
×[2-(-3)2].
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知函数![]() 的图象与x轴、y轴分别交于点A,B,与函数y=x的图象交于点M,点M的横坐标为2.在x轴上有一点P (a,0)(其中a>2),过点P作x轴的垂线,分别交函数
的图象与x轴、y轴分别交于点A,B,与函数y=x的图象交于点M,点M的横坐标为2.在x轴上有一点P (a,0)(其中a>2),过点P作x轴的垂线,分别交函数![]() 和y=x的图象于点C,D.
和y=x的图象于点C,D.
(1)求点A的坐标;
(2)若OB=CD,求a的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com