

���� ��1������B����������12����ռ�İٷֱ���30%���ݴ˼��������������
��2�����ñ��γ������Ե�ѧ���������Զ�Ӧ�İٷֱȼ������C����������������ȫֱ��ͼ��
��3��������״ͼ���оٳ����п��ܵĽ����Ȼ�����ø��ʹ�ʽ������⣮
��� �⣺��1�����γ������Ե�ѧ�������ǣ�12��30%=40���ˣ���
�ʱ��γ������Ե�ѧ������Ϊ40�ˣ�
��2��C���������ǣ�40��35%=14���ˣ���
��ͼ��ʾ��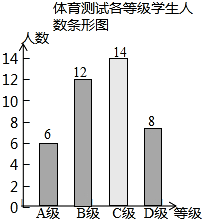
��3������λͬѧ�ֱ��ΪE��F��G��H������EΪС�����������⻭����ͼ���£�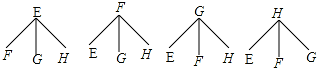
����12�������ѡ��С������6�֣�
��P��ѡ��С����=$\frac{6}{12}$=$\frac{1}{2}$��
���� ���⿼���������ͳ��ͼ������ͳ��ͼ���ۺ����ã�����ͳ��ͼ���Ӳ�ͬ��ͳ��ͼ�еõ���Ҫ����Ϣ�ǽ������Ĺؼ�������ͳ��ͼ������ر�ʾ��ÿ����Ŀ�����ݣ�����ͳ��ͼֱ�ӷ�ӳ����ռ����İٷֱȴ�С��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -4��-3 | B�� | 4��3 | C�� | 6��1 | D�� | -6��-1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
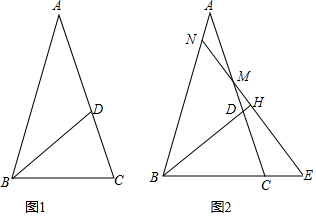
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
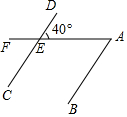 ��ͼ��ֱ��AB��CD��AF��CD�ڵ�E����DEF=140�㣬���A�Ķ����ǣ�������
��ͼ��ֱ��AB��CD��AF��CD�ڵ�E����DEF=140�㣬���A�Ķ����ǣ�������| A�� | 140�� | B�� | 40�� | C�� | 50�� | D�� | 60�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2016 | B�� | -2016 | C�� | $\frac{1}{2016}$ | D�� | -$\frac{1}{2016}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
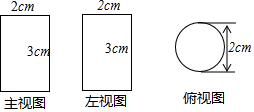 ��ͼΪһ�������������ͼ��
��ͼΪһ�������������ͼ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ѡ�QQ��Ц������ƽ��ֱ������ϵ�У���֪�۾�A��B������ֱ�Ϊ��-2��3������0��3��������C�������ǣ�-1��1����
��ͼ���ѡ�QQ��Ц������ƽ��ֱ������ϵ�У���֪�۾�A��B������ֱ�Ϊ��-2��3������0��3��������C�������ǣ�-1��1�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
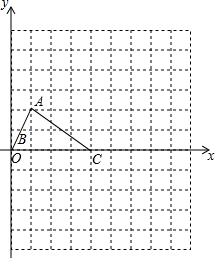 ��ͼ��һ��������������ÿһ��С�����εı߳�����1����λ���ȣ�ͼ�еġ�ABC�Ǹ�������Σ���B������ԭ���ϣ�
��ͼ��һ��������������ÿһ��С�����εı߳�����1����λ���ȣ�ͼ�еġ�ABC�Ǹ�������Σ���B������ԭ���ϣ��鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com