
分析 (1)根据运送单价乘以运送数量等于运费,可得函数解析式;
(2)根据运费不低于15160元,可得不等式,根据解不等式,可得答案,再根据一次函数的性质,可得答案.
解答 解:(1)设郑州运送省内该跑步机x台,郑州省外运送该跑步机(30-x)台,南阳运送省内运该跑步机(34-x),南阳省外送全部跑步机(6+x)台,根据题意,得
w=200x+250(30-x)+150(34-x)+240(6+x)
化简,得
w=40x+14040,
(2)由题意,得
40x+14040≥15160,
解得x≥28,
方案有:郑州运送省内该跑步机28台,郑州省外运送该跑步机2台,南阳运送省内运该跑步机6,南阳省外送全部跑步机34台;
郑州运送省内该跑步机29台,郑州省外运送该跑步机1台,南阳运送省内运该跑步机5,南阳省外送全部跑步机35台;
郑州运送省内该跑步机30台,郑州省外运送该跑步机0台,南阳运送省内运该跑步机4,南阳省外送全部跑步机36台;
w=40x+14040,
k=40>0,w随x的增大而减小,
x=28时,w最小是15160元.
点评 本题考查了一次函数的应用,解(1)的关键是利用运送单价乘以运送数量得出函数解析式;解(2)的关键是利用不等式的意义得出运送方案,又利用了一次函数的性质.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,方格纸中每个小正方形的边长都是1个单位长度,△ABC在平面直角坐标系中的位置如图所示.
如图,方格纸中每个小正方形的边长都是1个单位长度,△ABC在平面直角坐标系中的位置如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
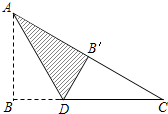 如图,Rt△ABC中,∠B=90°,AB=3,BC=4,将△ABC折叠,使点B恰好落在斜边AC上,与点B′重合,AD为折痕,求DB′的长.
如图,Rt△ABC中,∠B=90°,AB=3,BC=4,将△ABC折叠,使点B恰好落在斜边AC上,与点B′重合,AD为折痕,求DB′的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
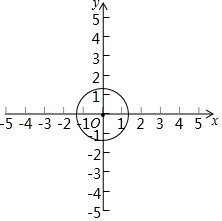 在平面直角坐标系中,我们不妨把横坐标与纵坐标相等的点称为梦之点,例如,点(1,1),(-2,-2),( $\sqrt{2}$,$\sqrt{2}$ ),…,都是梦之点,显然梦之点有无数个.
在平面直角坐标系中,我们不妨把横坐标与纵坐标相等的点称为梦之点,例如,点(1,1),(-2,-2),( $\sqrt{2}$,$\sqrt{2}$ ),…,都是梦之点,显然梦之点有无数个.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
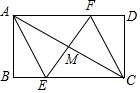 如图,在一张矩形纸片内,先折出矩形的对角线AC,以AC为折痕折叠AD交BC边于点E,再以AC为折痕折叠BC交AD边于点F,则下列结论不一定正确的是( )
如图,在一张矩形纸片内,先折出矩形的对角线AC,以AC为折痕折叠AD交BC边于点E,再以AC为折痕折叠BC交AD边于点F,则下列结论不一定正确的是( )| A. | AE=CF | B. | AB=AM | C. | AC⊥EF | D. | EF平分∠AEC |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com