
 如图,直线OC、BC的函数关系式分别是y1=x和y2=-2x+6,动点P(x,0)在OB上运动(0<x<3),过点P作直线m与x轴垂直.
如图,直线OC、BC的函数关系式分别是y1=x和y2=-2x+6,动点P(x,0)在OB上运动(0<x<3),过点P作直线m与x轴垂直.分析 (1)根据线OC、BC的函数关系式分别是y1=x和y2=-2x+6,即可求得点B、点C的坐标,和△COB的面积;
(2)当y1=y2时,x=-2x+6;当y1>y2时,x>-2x+6,分别解方程和不等式即可得出x的取值情况;
(3)当x为1时,y1=x=1,进而得到Q(1,1),P(1,0),据此求得△OPQ的面积即可;
(4)有两种情况:①当0<x≤2,此时直线m左侧部分是△PQO,由于P(x,0)在OB上运动,所以PQ,OP都可以用x表示,所以s与x之间函数关系式即可求出;②当2<x<3,此时直线m左侧部分是四边形OPQC,可运用割补法进行计算求解.
解答 解:(1)在直线y2=-2x+6中,令y=0,则x=3,
∴B(3,0),即OB=3,
解方程组$\left\{\begin{array}{l}{y=x}\\{y=-2x+6}\end{array}\right.$,得$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$,
∴C点坐标为(2,2),
∴△COB的面积=$\frac{1}{2}$×3×2=3;
(2)当y1=y2时,x=-2x+6,
解得x=2,
当y1>y2时,x>-2x+6,
解得x>2,
故当x取2时y1=y2;当x>2时,y1>y2;
(3)当x为1时,y1=x=1,
∴Q(1,1),P(1,0),
∴△OPQ的面积=$\frac{1}{2}$×1×1=$\frac{1}{2}$;
(4)分两种情况:
①如图所示,当0<x≤2时,则可得OP=x,EP=x,
此时s=$\frac{1}{2}$OP×PE=$\frac{1}{2}$x2;
②如图所示,当2<x<3时,过点C作CF⊥x轴于F,则CF=2=OF,EP=-2x+6,PF=x-2,
∴S△OCF=$\frac{1}{2}$OF×CF=2,
S梯形EPFC=$\frac{1}{2}$(EP+CF)×FP=$\frac{1}{2}$(-2x+6+2)×(x-2)=-x2+6x-8.
∴S=S△OCF+S梯形EPFC=2+(-x2+6x-8)=-x2+6x-6,
综上所述,S与x的函数关系式为:S=$\left\{\begin{array}{l}{\frac{1}{2}{x}^{2}(0<x≤2)}\\{-{x}^{2}+6x-6(2<x<3)}\end{array}\right.$.
点评 此题属于三角形综合题,主要考查平面直角坐标系中图形的面积的求法以及一次函数的应用.解答此题的关键是根据一次函数的特点,分别求出各点的坐标再得出线段的长.解题的难点在第(4)问,关键是根据点C的坐标,分段求出s与x的关系式.解题时注意分类思想和数形结合思想的运用.


科目:初中数学 来源: 题型:解答题
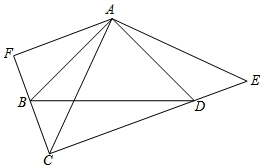 如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CF,垂足为F.
如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CF,垂足为F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 5 | C. | $\frac{13}{7}$ | D. | $\frac{13}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | -$\frac{2}{3}$ | D. | -$\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在四边形ABCD中,AD平行且等于BC,AB平行且等于DC,AD⊥AB,E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,连结AP并延长AP交CD于F点.
如图,在四边形ABCD中,AD平行且等于BC,AB平行且等于DC,AD⊥AB,E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,连结AP并延长AP交CD于F点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
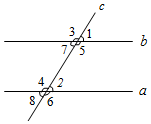 如图,直线a、b都与直线c相交,有下列条件:①∠1=∠2;②∠3+∠8=180°;③∠4=∠5;④∠6+∠7=180°.其中,能够判断a∥b的是( )
如图,直线a、b都与直线c相交,有下列条件:①∠1=∠2;②∠3+∠8=180°;③∠4=∠5;④∠6+∠7=180°.其中,能够判断a∥b的是( )| A. | ①② | B. | ②③④ | C. | ①③ | D. | ①②③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com