
【题目】如图,在□![]() 中,
中, ![]() 是
是![]() 上一点,且
上一点,且![]() ,
,![]() 与
与![]() 的延长线交点
的延长线交点![]() .
.
(1)求证:△![]() ∽△
∽△![]() ;
;
(2)若△![]() 的面积为1,求□
的面积为1,求□ ![]() 的面积.
的面积.

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
【题目】为加快5G网络建设,某移动通信公司在山顶上建了一座5G信号通信塔AB,山高BE=100米(A,B,E在同一直线上),点C与点D分别在E的两侧(C,E,D在同一直线上),BE⊥CD,CD之间的距离1000米,点D处测得通信塔顶A的仰角是30°,点C处测得通信塔顶A的仰角是45°(如图),则通信塔AB的高度约为( )米.(参考数据:![]() ,
,![]() )
)
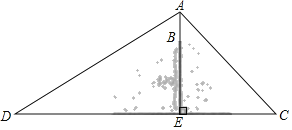
A.350B.250C.200D.150
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AE,CF分别是∠BAD和∠BCD的平分线,添加一个条件,仍无法判断四边形AECF为菱形的是( )
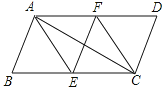
A. AE=AFB. EF⊥ACC. ∠B=60°D. AC是∠EAF的平分线
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为激发学生的阅读兴趣,培养学生良好的阅读习惯,我区某校欲购进一批学生喜欢的图书,学校组织学生会随机抽取部分学生进行问卷调查,被调查学生须从“文史类、社科类、小说类、生活类”中选择自己喜欢的一类,根据调查结果绘制了统计图(未完成),请根据图中信息,解答下列问题:
(1)填空或选择:此次共调查了______名学生;图2中“小说类”所在扇形的圆心角为______度;学生会采用的调查方式是______.A.普查 B.抽样调查
(2)将条形统计图(图1)补充完整;
(3)若该校共有学生2500人,试估计该校喜欢“社科类”书籍的学生人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD⊥BC于点D,点E是线段AD上的一个动点,连接EC,线段EC绕点E顺时针旋转60°得到线段EF,连接DF、BF,已知AD=5cm,BC=8cm,设AE=xcm,DF=y1cm,BF=y2cm.小王根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.
下面是小王的探究过程,请补充完整:
(1)对照下表中自变量x的值进行取点,画图,测量,分别得到了y1,y2与x的几组对应值:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 |
y1/cm | 2.52 | 2.07 | 2.05 | 2.48 |
| 4.00 |
y2/cm | 1.93 | 2.93 | 3.93 | 4.93 | 5.93 | 6.93 |
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),(x,y2),并画出函数y1,y2的图象:

(3)结合函数图象,解决问题:
①当AE的长度约为_______cm时,DF最小;
②当△BDF是以BF为腰的等腰三角形时,AE的长度约为______cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的对角线OB,AC相交于点D,且BE∥AC,AE∥OB,
(1)求证:四边形AEBD是菱形;
(2)如果OA=3,OC=2,求出经过点E的反比例函数解析式.
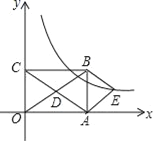
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,其对称轴与
,其对称轴与![]() 轴交于点
轴交于点![]() .
.
(1)求点![]() 、
、![]() 的坐标.
的坐标.
(2)若直线![]() 与直线
与直线![]() 关于该抛物线的对称轴对称,该抛物线在
关于该抛物线的对称轴对称,该抛物线在![]() 这一段位于直线
这一段位于直线![]() 的上方,并且在
的上方,并且在![]() 这一段位于直线
这一段位于直线![]() 的下方,求该抛物线的解析式.
的下方,求该抛物线的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com