
ЁОЬтФПЁПЮЊСЫНтФГаЃЁАдФЖСЙЄГЬЁБЕФПЊеЙЧщПіЃЌЧјНЬг§ОжДгИУаЃГѕжаЩњжаЫцЛњГщШЁСЫ150УћбЇЩњНјааСЫдФЖСЧщПіЕФЕїВщЮЪОэЃЌВЂЛцжЦСЫШчЭМЫљЪОВЛЭъећЕФЭГМЦЭМЃК
ИљОнЩЯЪіЭГМЦЭМЬсЙЉЕФаХЯЂЃЌЛиД№ЯТСаЮЪЬтЃК
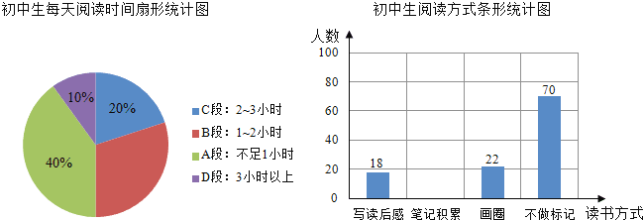
ЃЈ1ЃЉГѕжаЩњУПЬьдФЖСЪБМфдкФФвЛЖЮЕФШЫЪ§зюЖрЃПУПЬьдФЖСЪБМфдкBЖЮЕФЩШаЮЕФдВаФНЧЪЧЖрЩйЖШ?
ЃЈ2ЃЉШєНЋаДЖСКѓИаЁЂБЪМЧЛ§РлЁЂЛШІЕуЖСШ§жжЗНЪНГЦЮЊгаМЧвфдФЖСЃЌЧѓБЪМЧЛ§РлШЫЪ§еМгаМЧвфдФЖСШЫЪ§ЕФАйЗжБШЃЌВЂВЙШЋЬѕаЮЭГМЦЭМ.
ЁОД№АИЁПЃЈ1ЃЉГѕжаЩњУПЬьдФЖСЪБМфВЛзу1аЁЪБЕФШЫЪ§зюЖрЃЛУПЬьдФЖСЪБМфдкBЖЮЕФЩШаЮЕФдВаФНЧЪЧ108ЁуЃЛЃЈ2ЃЉБЪМЧЛ§РлШЫЪ§еМгаМЧвфдФЖСШЫЪ§ЕФАйЗжБШЮЊ50%ЃЌВЙШЋЬѕаЮЭГМЦЭММћНтЮі.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЩШаЮЭГМЦЭМЕУГіУПЬьдФЖСЪБМфдкВЛзу1аЁЪБЕФШЫЪ§зюЖрЃЛгЩзмбЇЩњЪ§МѕШЅЦфжаЕФЧѓГіБЪМЧЛ§РлЕФбЇЩњЪ§ЃЌЧѓГіBЖЮеМЕФАйЗжБШЃЌГЫвд360ЁуМДПЩЕУЕННсЙћЃЛ
ЃЈ2ЃЉЧѓГіБЪМЧЛ§РлеМаДЖСКѓИаЁЂБЪМЧЛ§РлЁЂЛШІЕуЖСШ§жжЗНЪНзмШЫЪ§ЕФАйЗжБШЃЌВЙШЋЬѕаЮЭГМЦЭММДПЩЃЎ
НтЃКЃЈ1ЃЉИљОнЩШаЮЭГМЦЭМЕУЃКГѕжаЩњУПЬьдФЖСЪБМфВЛзу1аЁЪБЕФШЫЪ§зюЖрЃЛ
дФЖСЪБМфдкBЖЮЕФЩШаЮдВаФНЧЮЊЃЈ1-10%-20%-40%ЃЉЁС360Ёу=108ЁуЃЛ
ЃЈ2ЃЉИљОнЬтвтЕУЃК150-ЃЈ18+22+70ЃЉ=40ЃЈШЫЃЉЃЌБЪМЧЛ§РлбЇЩњга40ШЫЃЌ
ИљОнЬтвтЕУЃК![]() ЁС100%=50%ЃЌ
ЁС100%=50%ЃЌ
дђБЪМЧЛ§РлШЫЪ§еМгаМЧвфдФЖСШЫЪ§ЕФАйЗжБШЮЊ50%.
ВЙШЋЬѕаЮЭГМЦЭМЃЌШчЭМЫљЪОЃЎ



 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЗНЗЈИаЮђЃК
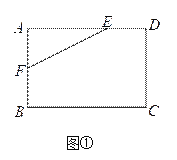
ЃЈ1ЃЉШчЭМЂйЃЌдкОиаЮABCDжаЃЌAB=4ЃЌAD=6ЃЌAE=4ЃЌAF=2ЃЌЪЧЗёдкБпBCЁЂCDЩЯЗжБ№ДцдкЕуGЁЂHЃЌЪЙЕУЫФБпаЮEFGHЕФжмГЄзюаЁЃПШєДцдкЃЌЧѓГіЫќжмГЄЕФзюаЁжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЮЪЬтНтОіЃК
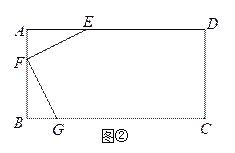
ЃЈ2ЃЉШчЭМЂкЃЌгавЛОиаЮАхВФABCDЃЌAB=3УзЃЌAD=6УзЃЌЯжЯыДгДЫАхВФжаВУГівЛИіУцЛ§ОЁПЩФмДѓЕФЫФБпаЮEFGHВПМўЃЌЪЙЁЯEFG=90ЁуЃЌEF=FG=![]() УзЃЌЁЯEHG=45ЁуЃЌОбаОПЃЌжЛгаЕБЕуEЁЂFЁЂGЗжБ№дкБпADЁЂABЁЂBCЩЯЃЌЧвAFЃМBFЃЌВЂТњзуЕуHдкОиаЮABCDФкВПЛђБпЩЯЪБЃЌВХгаПЩФмВУГіЗћКЯвЊЧѓЕФВПМўЃЌЪдЮЪФмЗёВУЕУЗћКЯвЊЧѓЕФУцЛ§ОЁПЩФмДѓЕФЫФБпаЮEFGHВПМўЃПШєФмЃЌЧѓГіВУЕУЕФЫФБпаЮEFGHВПМўЕФУцЛ§ЃЌВЂаДГідквдBЮЊзјБъдЕуЃЌжБЯпBCЮЊxжсЃЌжБЯпBAЮЊyжсЕФзјБъЯЕжаЃЌЕуHЕФзјБъЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
УзЃЌЁЯEHG=45ЁуЃЌОбаОПЃЌжЛгаЕБЕуEЁЂFЁЂGЗжБ№дкБпADЁЂABЁЂBCЩЯЃЌЧвAFЃМBFЃЌВЂТњзуЕуHдкОиаЮABCDФкВПЛђБпЩЯЪБЃЌВХгаПЩФмВУГіЗћКЯвЊЧѓЕФВПМўЃЌЪдЮЪФмЗёВУЕУЗћКЯвЊЧѓЕФУцЛ§ОЁПЩФмДѓЕФЫФБпаЮEFGHВПМўЃПШєФмЃЌЧѓГіВУЕУЕФЫФБпаЮEFGHВПМўЕФУцЛ§ЃЌВЂаДГідквдBЮЊзјБъдЕуЃЌжБЯпBCЮЊxжсЃЌжБЯпBAЮЊyжсЕФзјБъЯЕжаЃЌЕуHЕФзјБъЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁРђЕФАжАжТђСЫШЅПДжаЙњРКЧђжАвЕСЊШќзмОіШќЕФвЛеХУХЦБЃЌЫ§КЭИчИчСНШЫЖМКмЯыШЅЙлПДЃЌПЩУХЦБжЛгавЛеХЃЌЖСОХФъМЖЕФИчИчЯыСЫвЛИіАьЗЈЃЌФУСЫАЫеХЦЫПЫХЦЃЌНЋЪ§зжЮЊ1ЃЌ2ЃЌ3ЃЌ5ЕФЫФеХХЦИјаЁРђЃЌНЋЪ§зжЮЊ4ЃЌ6ЃЌ7ЃЌ8ЕФЫФеХХЦСєИјздМКЃЌВЂАДШчЯТгЮЯЗЙцдђНјааЃКаЁРђКЭИчИчДгИїздЕФЫФеХХЦжаЫцЛњГщГівЛеХЃЌШЛКѓНЋГщГіЕФСНеХЦЫПЫХЦЪ§зжЯрМгЃЌШчЙћКЭЮЊХМЪ§ЃЌдђаЁРђШЅЃЛШчЙћКЭЮЊЦцЪ§ЃЌдђИчИчШЅЃЎ
ЃЈ1ЃЉЧыгУСаБэЕФЗНЗЈЧѓаЁРђШЅПДжаЙњРКЧђжАвЕСЊШќзмОіШќЕФИХТЪЃЛ
ЃЈ2ЃЉИчИчЩшМЦЕФгЮЯЗЙцдђЙЋЦНТ№ЃПШєЙЋЦНЃЌЧыЫЕУїРэгЩЃЛШєВЛЙЋЦНЃЌЧыФуЩшМЦвЛжжЙЋЦНЕФгЮЯЗЙцдђЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃбЇЩњРћгУЫЋанЪБМфШЅОрбЇаЃ10 kmЕФЬьЦНЩНЩчЛсЪЕМљЛюЖЏЃЌвЛВПЗжбЇЩњЦяЕчЦПГЕЯШзпЃЌЙ§СЫ20 minКѓЃЌЦфгрбЇЩњГЫЙЋНЛГЕбиЯрЭЌТЗЯпГіЗЂЃЌНсЙћЫћУЧЭЌЪБЕНДяЃЎвбжЊЙЋНЛГЕЕФЫйЖШЪЧЕчЦПГЕбЇЩњЫйЖШЕФ2БЖЃЌЧѓЦяЕчЦПГЕбЇЩњЕФЫйЖШКЭЙЋНЛГЕЕФЫйЖШЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊOЮЊжБЯпADЩЯвЛЕуЃЌOBЪЧЁЯAOCФкВПвЛЬѕЩфЯпЧвТњзуЁЯAOBгыЁЯAOCЛЅВЙЃЌOMЁЂONЗжБ№ЮЊЁЯAOCЁЂЁЯAOBЕФЦНЗжЯпЃЎ
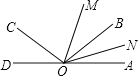
ЃЈ1ЃЉЁЯCODгыЁЯAOBЯрЕШТ№ЃПЧыЫЕУїРэгЩЃЛ
ЃЈ2ЃЉШєЁЯAOBЃН30ЁуЃЌЪдЧѓЁЯAOMгыЁЯMONЕФЖШЪ§ЃЛ
ЃЈ3ЃЉШєЁЯMONЃН55ЁуЃЌЪдЧѓЁЯAOCЕФЖШЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЬхг§гУЦЗЩЬЕъЪдЯњвЛПюГЩБОЮЊ 50 дЊЕФХХЧђЃЌЙцЖЈЪдЯњЦкМфЕЅМлВЛЕЭгкГЩБОМлЃЌЧвЛёРћВЛЕУИпгк 40%ЁЃОЪдЯњЗЂЯжЃЌЯњЪлСП ![]() ЃЈИіЃЉгыЯњЪлЕЅМл
ЃЈИіЃЉгыЯњЪлЕЅМл ![]() ЃЈдЊЃЉжЎМфТњзуШчЭМЫљЪОЕФвЛДЮКЏЪ§ЙиЯЕ.
ЃЈдЊЃЉжЎМфТњзуШчЭМЫљЪОЕФвЛДЮКЏЪ§ЙиЯЕ.
ЃЈ1ЃЉЪдШЗЖЈ![]() гы
гы ![]() жЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
жЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
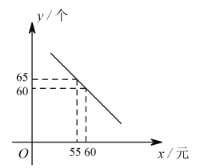
ЃЈ2ЃЉШєИУЬхг§гУЦЗЩЬЕъЪдЯњЕФетПюХХЧђЫљЛёЕУЕФРћШѓЮЊ ![]() дЊЃЌЪдаДГіРћШѓ
дЊЃЌЪдаДГіРћШѓ ![]() ЃЈдЊЃЉгыЯњЪлЕЅМл
ЃЈдЊЃЉгыЯњЪлЕЅМл ![]() ЃЈдЊЃЉжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛЕБЪдЯњЕЅМлЖЈЮЊЖрЩйдЊЪБЃЌИУЩЬЕъПЩЛёзюДѓРћШѓЃПзюДѓРћШѓЪЧЖрЩйдЊЃП
ЃЈдЊЃЉжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛЕБЪдЯњЕЅМлЖЈЮЊЖрЩйдЊЪБЃЌИУЩЬЕъПЩЛёзюДѓРћШѓЃПзюДѓРћШѓЪЧЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
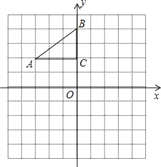
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌRtЁїABCЕФШ§ИіЖЅЕуЗжБ№ЪЧAЃЈЉ3ЃЌ2ЃЉЃЌBЃЈ0ЃЌ4ЃЉЃЌCЃЈ0ЃЌ2ЃЉЃЎ
ЃЈ1ЃЉНЋЁїABCвдЕуCЮЊа§зЊжааФа§зЊ180ЁуЃЌЛГіа§зЊКѓЖдгІЕФЁїA1B1CЃЛ
ЃЈ2ЃЉЦНвЦЁїABCЃЌШєЕуAЕФЖдгІЕуA2ЕФзјБъЮЊЃЈ0ЃЌЉ4ЃЉЃЌЛГіЦНвЦКѓЖдгІЕФЁїA2B2C2 ЃЛ
ЃЈ3ЃЉШєНЋЁїA1B1CШЦФГвЛЕуа§зЊПЩвдЕУЕНЁїA2B2C2,ЧыжБНгаДГіа§зЊжааФЕФзјБъ .
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЫЎЙћХњЗЂЪаГЁЙцЖЈЃЌвЛДЮЙКТђЦЛЙћВЛГЌЙ§100kgЃЈАќРЈ100kgЃЉЃЌХњЗЂМлЮЊ5дЊЃЌШчЙћвЛДЮЙКТђ100kgвдЩЯЦЛЙћЃЌГЌЙ§100kgЕФВПЗжЦЛЙћМлИёДђ8елЃЎ
ЃЈIЃЉЧыЬюаДЯТБэ
ЙКТђСП/kg | 0 | 50 | 100 | 150 | 200 | Ё |
ИЖПюН№Жю/дЊ | 0 | 250 | _ | 700 | __ | Ё |
ЃЈЂђЃЉаДГіИЖПюН№ЖюЙигкЙКТђСПЕФКЏЪ§НтЮіЪНЃЛ
ЃЈЂѓЃЉШчЙћФГШЫИЖПю2100дЊЃЌЧѓЦфЙКТђЦЛЙћЕФЪ§СПЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
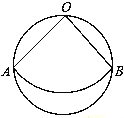
ЁОЬтФПЁПШчЭМЃЌДгжБОЖЮЊ2cmЕФдВаЮжНЦЌжаЃЌМєГівЛИідВаФНЧЮЊ90ЁуЕФЩШаЮOABЃЌЧвЕуOЁЂAЁЂBдкдВжмЩЯЃЌАбЫќЮЇГЩвЛИідВзЖЃЌдђдВзЖЕФЕзУцдВЕФАыОЖЪЧ cmЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com