
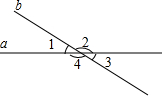
 如图,已知直线a、b相交,∠1=40°,求∠2、∠3、∠4的度数
如图,已知直线a、b相交,∠1=40°,求∠2、∠3、∠4的度数分析 先根据对顶角相等得到∠3=∠1=40°,然后根据邻补角的定义计算∠2与∠4;
变式1:根据∠2-∠1=40°,∠2+∠1=180°,即可求得∠2、∠3、∠4的度数;
变式2:根据∠2=3∠1,∠2+∠1=180°,即可求得∠2、∠3、∠4的度数;
变式3:根据∠1:∠2=2:9,∠2+∠1=180°,即可求得∠2、∠3、∠4的度数.
解答  解:∵∠1=40°,
解:∵∠1=40°,
∴∠3=∠1=40°,
∴∠2=∠4=180°-∠1=180°-40°=140°.
变式1:
∵∠2-∠1=40°,∠2+∠1=180°,
∴2∠2=220°,
∴∠2=110°,
∴∠4=110°,∠1=∠3=70°;
变式2:
∵∠2=3∠1,∠2+∠1=180°,
∴4∠1=180°,
∴∠1=45°,
∴∠3=45°,∠2=∠4=135°;
变式3:
∵∠1:∠2=2:9,∠2+∠1=180°,
∴∠2+$\frac{2}{9}$∠2=180°,
解得∠2=($\frac{1620}{11}$)°,
∴∠4=($\frac{1620}{11}$)°,∠1=∠3=180°-($\frac{1620}{11}$)°=($\frac{360}{11}$)°.
点评 本题考查了对顶角、邻补角的定义的运用,解题时注意:有一个公共顶点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种位置关系的两个角互为对顶角;只有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角互为邻补角.


科目:初中数学 来源: 题型:选择题
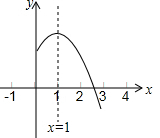 二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的对称轴是直线x=1,其图象的一部分如图所示,对于下列说法:
二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的对称轴是直线x=1,其图象的一部分如图所示,对于下列说法:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{18}$ | B. | $\frac{2}{15}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{12}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
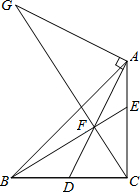 如图,Rt△ABC中,∠BCA=90°,AC=BC,点D是BC的中点,点F在线段AD上,DF=CD,BF交CA于E点,过点A作DA的垂线交CF的延长线于点G,下列结论:①CF2=EF•BF;②AG=2DC;③AE=EF;④AF•EC=EF•EB.其中正确的结论有①②④.
如图,Rt△ABC中,∠BCA=90°,AC=BC,点D是BC的中点,点F在线段AD上,DF=CD,BF交CA于E点,过点A作DA的垂线交CF的延长线于点G,下列结论:①CF2=EF•BF;②AG=2DC;③AE=EF;④AF•EC=EF•EB.其中正确的结论有①②④.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com