
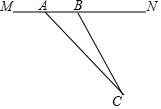
 目前,我市正在积极创建文明城市,交通部门一再提醒司机:为了安全,请勿超速,并再进一步完善各类监测系统,如图,在某公路直线路段MN内限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.(参考数据:$\sqrt{2}$=1.41,$\sqrt{3}$=1.73)
目前,我市正在积极创建文明城市,交通部门一再提醒司机:为了安全,请勿超速,并再进一步完善各类监测系统,如图,在某公路直线路段MN内限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.(参考数据:$\sqrt{2}$=1.41,$\sqrt{3}$=1.73) 分析 先构造出直角三角形,在Rt△BCH中,求出CH,BH,再在Rt△AHC中,求出AH,即可求出AB最后求出速度和行车速度比较即可.
解答 解:此车没有超速,
理由:如图,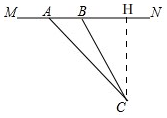 过点C作CH⊥MN于H,
过点C作CH⊥MN于H,
在Rt△BCH中,∠CBN=60°,BC=200,
∴CH=BC•sin60°=100$\sqrt{3}$米,BH=BC•cos60°=100米,
在Rt△AHC中,∠CAN=45°,
∴AH=CH=100$\sqrt{3}$米,
∴AB=AH-BH=100$\sqrt{3}$-100≈73米,
∴车速为$\frac{73}{5}$=14.6m/s,
∵60km/h=$\frac{50}{3}$m/s,而14.6<$\frac{50}{3}$,
∴此车没超速.
点评 此题是解直角三角形的应用,主要考查了锐角三角函数,解本题的关键是构造出直角三角形,是一道基础题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
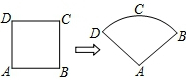 如图,某数学兴趣小组将边长为6的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形,则扇形的圆心角∠DAB的度数是$\frac{360}{π}$度.(结果保留π)
如图,某数学兴趣小组将边长为6的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形,则扇形的圆心角∠DAB的度数是$\frac{360}{π}$度.(结果保留π)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
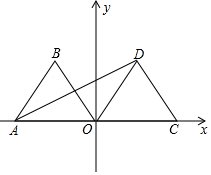 如图,在平面直角坐标系中,点A(-2,0),等边△AOB经过平移或轴对称或旋转都可以得到△OCD.
如图,在平面直角坐标系中,点A(-2,0),等边△AOB经过平移或轴对称或旋转都可以得到△OCD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
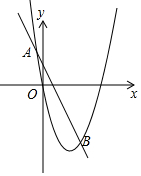 如图,在平面直角坐标系中,点A(-1,n)与点B(2,n),在抛物线y=x2-3x上,
如图,在平面直角坐标系中,点A(-1,n)与点B(2,n),在抛物线y=x2-3x上,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
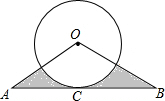 如图,在△ABC中,OA=OB=6,∠O=120°,以点O为圆心的⊙O和底边AB相切于点C,则阴影部分的面积为9$\sqrt{3}$-3π..
如图,在△ABC中,OA=OB=6,∠O=120°,以点O为圆心的⊙O和底边AB相切于点C,则阴影部分的面积为9$\sqrt{3}$-3π..查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com