
【题目】AD是△ABC的高,AC=2 ![]() ,AD=4,把△ADC沿着直线AD对折,点C落在点E的位置,如果△ABE是等腰三角形,那么线段BE的长度为( )
,AD=4,把△ADC沿着直线AD对折,点C落在点E的位置,如果△ABE是等腰三角形,那么线段BE的长度为( )
A.2 ![]()
B.2 ![]() 或5
或5
C.2 ![]()
D.5
【答案】B
【解析】解:如图 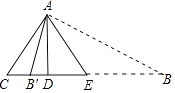
①当高AD在△ABC内时,由题意EA=EB=AC=2 ![]() .
.
②当高AD在△ACB′外时,设AB′=B′E=x.
在Rt△ADC中,CD= ![]() =
= ![]() =2,
=2,
由题意DE=DC=2,
在Rt△AED中,∵AB′2=AD2+DB′2 ,
∴x2=42+(x﹣2)2 ,
∴x=5.
∴线段BE的长度为2 ![]() 或5,
或5,
故选B.
【考点精析】本题主要考查了等腰三角形的性质和翻折变换(折叠问题)的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角);折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能正确解答此题.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两名射手在相同条件下打靶,射中的环数如图所示,利用图中提供的信息,解答下列问题:
(1)分别求甲、乙两名射手中环数的众数和平均数;
(2)如果从甲、乙两名射手中选一名去参加射击比赛,你选谁去?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠ABC=120°,BD平分∠ABC,∠DAC=60°,若AB=2,BC=3,则BD的长是( )
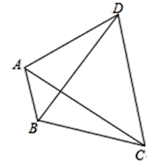
A. 5 B. 7 C. 8 D. 9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,一次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() .
.
(1)若点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() 在一次函数
在一次函数![]() 的图象上,求
的图象上,求![]() 的值;
的值;
(2)求由直线![]() ,(1)中的直线
,(1)中的直线![]() 以及
以及![]() 轴围成的三角形的面积.
轴围成的三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB和CD相交于O点,OE⊥CD,OC平分∠AOF,∠EOF=56°,
(1)求∠BOD的度数;
(2)写出图中所有与∠BOE互余的角,它们分别是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BF平分∠ABC,AF⊥BF于点F,D为AB的中点,连接DF延长交AC于点E.若AB=10,BC=18,则线段EF的长为( ) 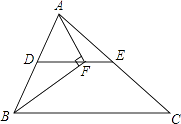
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(10,0),(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com