
如图,在正五边形ABCDE中,连接AC、AD、CE,CE交AD于点F,连接BF,下列说法不正确的是( )

|
| A. | △CDF的周长等于AD+CD | B. | FC平分∠BFD |
|
| C. | AC2+BF2=4CD2 | D. | DE2=EF•CE |
B解:∵五边形ABCDE是正五边形,
∴AB=BC=CD=DE=AE,BA∥CE,AD∥BC,AC∥DE,AC=AD=CE,
∴四边形ABCF是菱形,
∴CF=AF,
∴△CDF的周长等于CF+DF+CD,
即△CDF的周长等于AD+CD,
故A说法正确;
∵四边形ABCF是菱形,
∴AC⊥BF,
设AC与BF交于点O,
由勾股定理得OB2+OC2=BC2,
∴AC2+BF2=(2OC)2+(2OB)2=4OC2+4OB2=4BC2,
∴AC2+BF2=4CD2.
故C说法正确;
由正五边形的性质得,△ADE≌△CDE,
∴∠DCE=∠EDF,
∴△CDE∽△DFE,
∴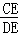 =
=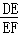 ,
,
∴DE2=EF•CE,


科目:初中数学 来源: 题型:
在矩形ABCD中,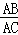 =a,点G,H分别在边AB,DC上,且HA=HG,点E为AB边上的一个动点,连接HE,把△AHE沿直线HE翻折得到△FHE.
=a,点G,H分别在边AB,DC上,且HA=HG,点E为AB边上的一个动点,连接HE,把△AHE沿直线HE翻折得到△FHE.
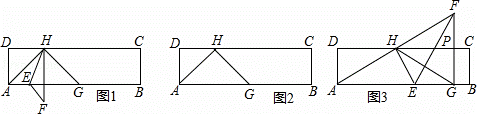
(1)如图1,当DH=DA时,
①填空:∠HGA= 45 度;
②若EF∥HG,求∠AHE的度数,并求此时的最小值;
(2)如图3,∠AEH=60°,EG=2BG,连接FG,交边FG,交边DC于点P,且FG⊥AB,G为垂足,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图1,在⊙O中,E是弧AB的中点,C为⊙O上的一动点(C与E在AB异侧),连接EC交AB于点F,EB= (r是⊙O的半径).
(r是⊙O的半径).
(1)D为AB延长线上一点,若DC=DF,证明:直线DC与⊙O相切;
(2)求EF•EC的值;
(3)如图2,当F是AB的四等分点时,求EC的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
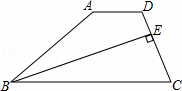
如图,在梯形ABCD中,AD∥BC,BE平分∠ABC交CD于E,且BE⊥CD,CE:ED=2:1.如果△BEC的面积为2,那么四边形ABED的面积是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com