
【题目】下列方程中解为![]() 的方程是( )
的方程是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
分别将x=2代入或解方程即可.
A. 把x=2代入方程的左边为:![]() ,代入右边为:
,代入右边为:![]() ,左边不等于右边,所以x=2不是
,左边不等于右边,所以x=2不是![]() 的解,故A选项错误;
的解,故A选项错误;
B. 把x=2代入方程的左边为:2![]() (-1)=-2,代入右边为:-2+1=-1,左边不等于右边,所以x=2不是2(x-3)=-x+1的解,故B选项错误;
(-1)=-2,代入右边为:-2+1=-1,左边不等于右边,所以x=2不是2(x-3)=-x+1的解,故B选项错误;
C. 把x=2代入方程的左边为:2![]() 2+1=5,代入右边为:3
2+1=5,代入右边为:3![]() 2-1=5,左边等于右边,所以x=2是2x+1=3x-1的解,故C选项正确;
2-1=5,左边等于右边,所以x=2是2x+1=3x-1的解,故C选项正确;
D. 把x=2代入方程的左边为:3![]() (1-4)-2
(1-4)-2![]() 4=-17,代入右边为:0,左边不等于右边,所以x=2不是3(1-2x)-2(x+2)=0的解,故D选项错误.
4=-17,代入右边为:0,左边不等于右边,所以x=2不是3(1-2x)-2(x+2)=0的解,故D选项错误.
故选:C.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的一条弦,C是⊙O上一动点且∠ACB=45°,E,F分别是AC,BC的中点,直线EF与⊙O交于点G,H.若⊙O的半径为2,则GE+FH的最大值为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
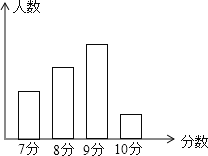
【题目】体育课上,体育老师对七年级一个班的学生进行了立定跳远项目的测试,得到一组测试分数的数据,并将测试所得分数绘制如图所示的统计图,图中从左到右的学生数人数之比为2 : 3 : 4 : 1,且成绩为8分的学生有12人,根据以上信息解答下列问题:
(1) 这个班级有多少名学生?
(2)这组数据的众数是 分,中位数是 分.
(3)这个班级学生立定跳远项目测试的平均成绩是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,经过点A(0,﹣4)的抛物线y= ![]() x2+bx+c与x轴相交于点B(﹣1,0)和C,O为坐标原点.
x2+bx+c与x轴相交于点B(﹣1,0)和C,O为坐标原点.
(1)求抛物线的解析式;
(2)将抛物线y= ![]() x2+bx+c向上平移
x2+bx+c向上平移 ![]() 个单位长度,再向左平移m(m>0)个单位长度,得到新抛物线,若新抛物线的顶点P在△ABC内,求m的取值范围;
个单位长度,再向左平移m(m>0)个单位长度,得到新抛物线,若新抛物线的顶点P在△ABC内,求m的取值范围;
(3)将x轴下方的抛物线图象关于x轴对称,得到新的函数图象C,若直线y=x+k与图象C始终有3个交点,求满足条件的k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的个数是( )
(1)﹣a表示负数;
(2)多项式﹣3a2b+7a2b2﹣2ab+l的次数是3;
(3)单项式﹣![]() 的系数为﹣2;
的系数为﹣2;
(4)一个有理数不是整数就是分数
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作ABDE,连接AD,EC.
(1)求证:△ADC≌△ECD;
(2)若BD=CD,求证:四边形ADCE是矩形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“囧”像一个人脸郁闷的神情.如图,边长为a的正方形纸片,剪去两个一样的小直角三角形(阴影部分)和一个长方形(阴影部分)得到一个“囧”字图案,设剪去的两个小直角三角形的两直角边长分别为x、y,剪去的小长方形长和宽也分别为x,y.
(1)用含a、x、y的式子表示“囧”的面积;
(2)当a=12,x=7,y=4时,求该图形面积的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数y=x2+bx+c的图象与x轴交于A,B两点,其中A点坐标为(﹣3,0),与y轴交于点C,点D(﹣2,﹣3)在抛物线上. 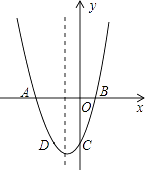
(1)求抛物线的解析式;
(2)抛物线的对称轴上有一动点P,求出PA+PD的最小值;
(3)若抛物线上有一动点P,使三角形ABP的面积为6,求P点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com